
【题目】交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为![]() ,其范围为
,其范围为![]() ,分别有五个级别:
,分别有五个级别:![]() 畅通;
畅通;![]() 基本畅通;
基本畅通;![]() 轻度拥堵;
轻度拥堵;![]() 中度拥堵;
中度拥堵;![]() 严重拥堵.晚高峰时段(
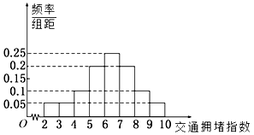
严重拥堵.晚高峰时段(![]() ),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示.
),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示.
(Ⅰ)用分层抽样的方法从交通指数在![]() ,
,![]() ,
,![]() 的路段中共抽取
的路段中共抽取![]() 个路段,求依次抽取的三个级别路段的个数;
个路段,求依次抽取的三个级别路段的个数;
(Ⅱ)从(Ⅰ)中抽出的![]() 个路段中任取
个路段中任取![]() 个,求至少有
个,求至少有![]() 个路段为轻度拥堵的概率.
个路段为轻度拥堵的概率.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)分别求![]() ,
,![]() ,
,![]() 这三个级别的路段,然后求抽样比,再求三个级别抽取的路段的个数;
这三个级别的路段,然后求抽样比,再求三个级别抽取的路段的个数;
(Ⅱ)根据(Ⅰ)的结果,分别设![]() 个轻度拥堵路段为
个轻度拥堵路段为![]() ,
,![]() ,选取的
,选取的![]() 个中度拥堵路段为
个中度拥堵路段为![]() ,
,![]() ,
,![]() ,选取的
,选取的![]() 个严重拥堵路段为
个严重拥堵路段为![]() ,然后按照列举法求概率.
,然后按照列举法求概率.
(Ⅰ)由直方图可知:
![]() ,
,![]() ,
,![]() .
.
所以这20个路段中,轻度拥堵、中度拥堵、严重拥堵路段分别为6个,9个,3个.
拥堵路段共有![]() 个,按分层抽样从18个路段中选出6个,
个,按分层抽样从18个路段中选出6个,
每种情况分别为:![]() ,
,![]() ,
,![]() ,
,
即这三个级别路段中分别抽取的个数为![]() .
.
(Ⅱ)记(Ⅰ)中选取的![]() 个轻度拥堵路段为
个轻度拥堵路段为![]() ,
,![]() ,选取的
,选取的![]() 个中度拥堵路段为
个中度拥堵路段为![]() ,
,![]() ,
,![]() ,选取的
,选取的![]() 个严重拥堵路段为
个严重拥堵路段为![]() ,则从
,则从![]() 个路段选取
个路段选取![]() 个路段的可能情况如下:
个路段的可能情况如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15种可能,
,共15种可能,
其中至少有![]() 个轻度拥堵的有:
个轻度拥堵的有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共9种可能,所以所选
,共9种可能,所以所选![]() 个路段中至少
个路段中至少![]() 个路段轻度拥堵的概率为:
个路段轻度拥堵的概率为:![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为200元,低于100箱按原价销售;不低于100箱通过双方议价,买方能以优惠![]() 成交的概率为0.6,以优惠
成交的概率为0.6,以优惠![]() 成交的概率为0.4.
成交的概率为0.4.
(1)甲、乙两单位都要在该厂购买150箱这种零件,两单位各自达成的成交价相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
(2)某单位需要这种零件650箱,求购买总价![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂过去在生产过程中将污水直接排放到河流中对沿河环境造成了一定的污染,根据环保部门对该厂过去10年的监测数据,统计出了其每年污水排放量![]() (单位:吨)的频率分布表:
(单位:吨)的频率分布表:
污水排放量 |
|
|
|
|
频率 | 0.1 | 0.3 | 0.4 | 0.2 |
将污水排放量落入各组的频率作为概率,并假设每年该厂污水排放量相互独立.
(1)若不加以治理,根据上表中的数据,计算未来3年中至少有2年污水排放量不小于200吨的概率;
(2)根据环保部门的评估,该厂当年污水排放量![]() 时,对沿河环境及经济造成的损失为5万元;当年污水排放量
时,对沿河环境及经济造成的损失为5万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为10万元;当年污水排放量
时,对沿河环境及经济造成的损失为10万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为20万元;当年污水排放量
时,对沿河环境及经济造成的损失为20万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
方案1:若该厂不采取治污措施,则需全部赔偿对沿河环境及经济造成的损失;
方案2:若该厂采购治污设备对所有产生的污水净化达标后再排放,则不需赔偿,采购设备的费用为10万元,每年设备维护等费用为15万元,该设备使用10年需重新更换.在接下来的10年里,试比较上述2种方案哪种能为该厂节约资金,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线C:y2=8x上一点A到焦点F的距离为6,若点P为抛物线C准线上的动点,则|OP|+|AP|的最小值为( )
A. 4B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某包子店每天早晨会提前做好若干笼包子,以保证当天及时供应,每卖出一笼包子的利润为40元,当天未卖出的包子作废料处理, 每笼亏损20元.该包子店记录了60天包子的日需求量![]() (单位:笼,
(单位:笼,![]() ),整理得到如图所示的条形图,以这60天各需求量的频率代替相应的概率.
),整理得到如图所示的条形图,以这60天各需求量的频率代替相应的概率.
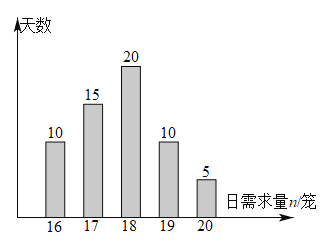
(1)设![]() 为一天的包子需求量,求
为一天的包子需求量,求![]() 的数学期望.
的数学期望.
(2)若该包子店想保证![]() 以上的天数能够足量供应,则每天至少要做多少笼包子?
以上的天数能够足量供应,则每天至少要做多少笼包子?
(3)为了减少浪费,该包子店一天只做18笼包子,设![]() 为当天的利润(单位:元),求
为当天的利润(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD所在平面垂直于直角梯形ABPE所在平面,EP![]() ,BP=2,AD=AE=1,AE⊥EP,AE∥BP,G,F分别是BP,BC的中点.
,BP=2,AD=AE=1,AE⊥EP,AE∥BP,G,F分别是BP,BC的中点.
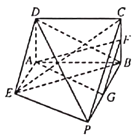
(1)求证:平面AFG∥平面PCE;
(2)求四棱锥D﹣ABPE的体积与三棱锥P﹣BCD的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,2Sn+2n=an+1﹣2,a2=8,其中n∈N*.
(1)记bn=an+1,求证:{bn}是等比数列;
(2)设![]() 为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身馆在2019年7、8两月推出优惠项目吸引了一批客户.为预估2020年7、8两月客户投入的健身消费金额,健身馆随机抽样统计了2019年7、8两月100名客户的消费金额,分组如下:![]() (单位:元),得到如图所示的频率分布直方图:
(单位:元),得到如图所示的频率分布直方图:
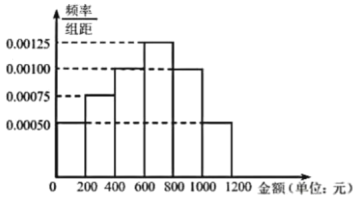
(1)若把2019年7、8两月健身消费金额不低于800元的客户,称为“健身达人”,经数据 处理,现在列联表中得到一定的相关数据,请补全空格处的数据,并根据列联表判断是否有![]() 的把握认为“健身达人”与性别有关?
的把握认为“健身达人”与性别有关?
健身达人 | 非健身达人 | 总计 | |
男 | 10 | ||
女 | 30 | ||
总计 |
(2)为吸引顾客,在健身项目之外,该健身馆特别推出健身配套营养品的销售,现有两种促销方案.
方案一:每满800元可立减100元;
方案二:金额超过800元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
若某人打算购买1000元的营养品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
(3)在(2)中的方案二中,金额超过800元可抽奖三次,假设三次中奖结果互不影响,且三次中奖的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,
的内角,
求证:![]()
附:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com