
如果函数 的图像与曲线
的图像与曲线 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
A
解析试题分析:解:由 可得,x≥0时,y=x-2;x<0时,y=-x-2,∴函数
可得,x≥0时,y=x-2;x<0时,y=-x-2,∴函数 的图象与方程x2+λy2=1的曲线必相交于(±1,0)所以为了使函数
的图象与方程x2+λy2=1的曲线必相交于(±1,0)所以为了使函数 图象与方程x2+λy2=1的曲线恰好有两个不同的公共点,则y=x-1代入方程x2+λy2=1,整理可得(1+λ)x2-2λx+λ-1=0,当λ=-1时,x=1满足题意,由于△>0,1是方程的根,∴
图象与方程x2+λy2=1的曲线恰好有两个不同的公共点,则y=x-1代入方程x2+λy2=1,整理可得(1+λ)x2-2λx+λ-1=0,当λ=-1时,x=1满足题意,由于△>0,1是方程的根,∴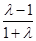 <0,即-1<λ<1时,方程两根异号,满足题意; y=-x-1代入方程x2+λy2=1,整理可得(1+λ)x2+2λx+λ-1=0,当λ=-1时,x=-1满足题意,由于△>0,-1是方程的根,∴
<0,即-1<λ<1时,方程两根异号,满足题意; y=-x-1代入方程x2+λy2=1,整理可得(1+λ)x2+2λx+λ-1=0,当λ=-1时,x=-1满足题意,由于△>0,-1是方程的根,∴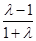 <0,即-1<λ<1时,方程两根异号,满足题意;,综上知,实数λ的取值范围是[-1,1),故选A
<0,即-1<λ<1时,方程两根异号,满足题意;,综上知,实数λ的取值范围是[-1,1),故选A
考点:圆锥曲线的定义和性质
点评:本题考查曲线的交点,考查学生分析解决问题的能力,考查分类讨论的数学思想,属于中档题


科目:高中数学 来源: 题型:单选题
已知双曲线 =1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
| A.[1,2] | B.(1,2) | C.[2,+∞) | D.(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com