
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线 ![]() =bx+a,其中b=
=bx+a,其中b= 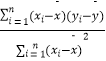 =
= 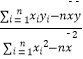 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
【答案】
(1)解:作出散点图如下:
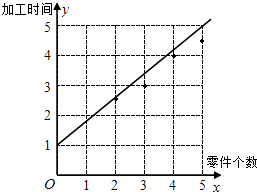
(2)解: ![]() =
= ![]() (2+3+4+5)=3.5,
(2+3+4+5)=3.5, ![]() =
= ![]() (2.5+3+4+4.5)=3.5,
(2.5+3+4+4.5)=3.5,
![]() =54,
=54, ![]() xiyi=52.5
xiyi=52.5
∴b= ![]() =0.7,a=3.5﹣0.7×3.5=1.05,
=0.7,a=3.5﹣0.7×3.5=1.05,
∴所求线性回归方程为:y=0.7x+1.05
(3)解:当x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时).
∴加工10个零件大约需要8.05个小时
【解析】(1)根据表中所给的数据,可得散点图;(2)求出出横标和纵标的平均数,得到样本中心点,求出对应的横标和纵标的积的和,求出横标的平方和,做出系数和a的值,写出线性回归方程.(3)将x=10代入回归直线方程,可得结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2 ![]() ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点. 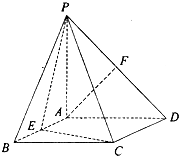
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD;
(3)求四面体PEFC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】机器人![]() (阿法狗)在下围棋时,令人称道的算法策略是:每一手棋都能保证在接下来的十几步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.
(阿法狗)在下围棋时,令人称道的算法策略是:每一手棋都能保证在接下来的十几步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.
下面的算法是寻找“![]() ”中“比较大的数
”中“比较大的数![]() ”,现输入正整数“42,61,80,12,79,18,82,57,31,18“,从左到右依次为
”,现输入正整数“42,61,80,12,79,18,82,57,31,18“,从左到右依次为![]() ,其中最大的数记为
,其中最大的数记为![]() ,则
,则![]() ( )
( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,k),
=(sinx,k), ![]() =(﹣2cosx,sinx﹣k).
=(﹣2cosx,sinx﹣k).
(1)当x∈[0, ![]() ]时,求|
]时,求| ![]() +
+ ![]() |的取值范围;
|的取值范围;
(2)若g(x)=( ![]() +
+ ![]() )
) ![]() ,求当k为何值时,g(x)的最小值为﹣
,求当k为何值时,g(x)的最小值为﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行六面体ABCD﹣A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( ) 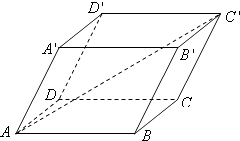
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)令![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象.区间
的图象.区间![]() 满足:
满足:![]() 在
在![]() 上至少含有30个零点.在所有满足上述条件的
上至少含有30个零点.在所有满足上述条件的![]() 中,求
中,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+3)=﹣f(x),且当x∈[0,3)时,f(x)=log4(x+1),给出下列命题:
①f(2015)>f(2014);
②函数f(x)在定义域上是周期为3的函数;
③直线x﹣3y=0与函数f(x)的图象有2个交点;
④函数f(x)的值域为[0,1).
其中不正确的命题个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com