
【题目】f(x)=lnx﹣ax+1.
(1)求f(x)的单调增区间.
(2)求出f(x)的极值.
【答案】
(1)解:f′(x)= ![]() ﹣a(x>0)
﹣a(x>0)
∴当a≤0时f′(x)>0恒成立,
∴f(x)的增区间为(0,+∞),
当a>0时,f′(x)>0的解为(0, ![]() ),
),
∴f(x)的增区间为(0, ![]() )
)
(2)解:f′(x)= ![]() ﹣a=0解得:x=
﹣a=0解得:x= ![]() ,
,
∴a>0时,x∈( ![]() ,+∞)时,f′(x)<0,
,+∞)时,f′(x)<0,
x∈(0, ![]() )时,f′(x)>0,
)时,f′(x)>0,
∴x= ![]() 是f(x)的极大值无极小值,
是f(x)的极大值无极小值,
当a≤0时,f′(x)>0恒成立,无极值
【解析】(1)求出函数的导数,通过讨论a的范围,求出函数的递增区间;(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的极值.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2+cx+d(a≠0)的对称中心为M(x0 , y0),记函数f(x)的导函数为f′(x),f′(x)的导函数为f″(x),则有f″(x0)=0.若函数f(x)=x3﹣3x2 , 则可求出f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )的值为( )
)的值为( )
A.4029
B.﹣4029
C.8058
D.﹣8058
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于两点
交于两点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校将高二年级某班级50位同学期中考试数学成绩(均为整数)分为7组![]() 进行统计,得到如图所示的频率分布直方图.观察图中信息,回答下列问题.
进行统计,得到如图所示的频率分布直方图.观察图中信息,回答下列问题.

(Ⅰ)试估计该班级同学数学成绩的平均分;
(Ⅱ)先准备从该班级数学成绩不低于130分的同学中随机选出2人参加某活动,求选出的两人在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
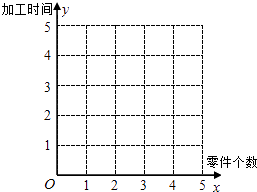
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线 ![]() =bx+a,其中b=
=bx+a,其中b= 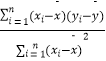 =
= 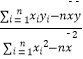 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的离心率是
的离心率是![]() ,且直线
,且直线![]() :
: ![]() 被椭圆
被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与圆
与圆![]() :
: ![]() 相切:
相切:
(i)求圆![]() 的标准方程;
的标准方程;
(ii)若直线![]() 过定点
过定点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,与圆
,与圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(kx+4)lnx﹣x(x>1),若f(x)>0的解集为(s,t),且(s,t)中只有一个整数,则实数k的取值范围为( )
A.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() )
)
B.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() ]
]
C.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1]
﹣1]
D.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1)
﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com