


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
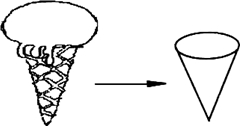 如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h.
如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h.| h |
| r |
查看答案和解析>>
科目:高中数学 来源: 题型:
 甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
2013 2014 |
3 5 |
1 n |
0 n-1 |
2 n |
1 n-1 |
3 n |
2 n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
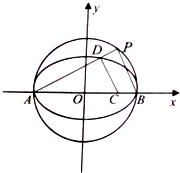 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com