
 已知抛物线y2=2px(p>0),点E(2,1),若斜率为2的弦过点E,且以E为弦中点.
已知抛物线y2=2px(p>0),点E(2,1),若斜率为2的弦过点E,且以E为弦中点.分析 (1)设弦的端点坐标为( x1,y1)、( x2,y2),则${y_1}^2=2p{x_1},\;\;{y_2}^2=2p{x_2}$,再根据弦的斜率为2求得p的值,可得抛物线方程.
(2)设A(x3,y3),B(x4,y4),把AB方程代入抛物线的方程,利用判别式大于零求得m的范围,再把MA的方程代入抛物线的方程,设出弦的端点坐标,利用韦达定理以及斜率公式求得该弦的斜率为定值.根据弦长公式求得弦长PQ的解析式,根据m的范围,利用不等式的性质求出|PQ|的取值范围.
解答 解:(1)设弦的端点坐标为( x1,y1)、( x2,y2),则${y_1}^2=2p{x_1},\;\;{y_2}^2=2p{x_2}$,
∴(y1+y2)(y1-y2)=2p(x1-x2).
又$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{2p}{{{y_1}+{y_2}}}=p$,求得p=2,抛物线方程为y2=4x.
(2)设A(x3,y3),B(x4,y4),AB方程:m(y+3)=x,代入y2=4x,y2-4my-12m=0,
由△>0,求得m<-3或m>0,y3+y4=4m,y3•y4=-12m.
由于点M(-1,0),直线AM:$y=\frac{y_1}{{{x_1}+1}}(x+1)$,由$\left\{\begin{array}{l}y=\frac{y_1}{{{x_1}+1}}(x+1)\\{y^2}=4x\end{array}\right.$,可得${y^2}-4•\frac{{{x_1}+1}}{y_1}y+4=0$,
∴${y_1}{y_p}=4,{y_p}=\frac{4}{y_1}$.
∴点$P(\frac{4}{{{y^2}_1}},\;\frac{4}{y_1}),Q(\frac{4}{{{y^2}_2}},\;\frac{4}{y_2})$,${k_{PQ}}=\frac{{\frac{4}{y_1}-\;\frac{4}{y_2}}}{{\frac{4}{{{y^2}_1}}-\frac{4}{{{y^2}_2}}}}=\frac{{{y_1}{y_2}}}{{{y_1}+{y_2}}}=\frac{-12m}{4m}=-3$,为定值.
∵$|PQ|=\sqrt{1+\frac{1}{k^2}}|{y_P}-{y_Q}|=\frac{{4\sqrt{10}}}{9}\sqrt{1+\frac{3}{m}}$.
由m<-3,或m>0,可得$|PQ|∈(0,\frac{{4\sqrt{10}}}{9})∪(\frac{{4\sqrt{10}}}{9},+∞)$.
点评 本题主要考查抛物线的标准方程的应用,直线的斜率公式,不等式的基本性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
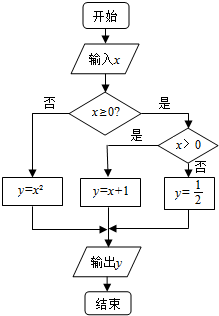
| A. | y=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{x+1,x<0}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{1}{2},x≥0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{\frac{1}{2},x=0}\\{x+1,x>0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{\frac{1}{2},x=0}\\{x+1,x<0}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.
如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (23,24) | B. | (24,27) | C. | (21,24) | D. | (24,25) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com