
已知椭圆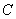 :
: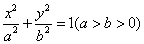 的离心率为
的离心率为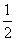 ,右焦点
,右焦点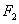 到直线
到直线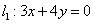 的距离为
的距离为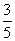 .
.
(Ⅰ)求椭圆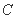 的方程;
的方程;
(Ⅱ)过椭圆右焦点F2斜率为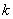 (
(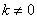 )的直线
)的直线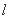 与椭
与椭 圆
圆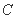 相交于
相交于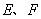 两点,
两点,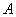 为椭圆的右顶点,直线
为椭圆的右顶点,直线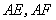 分别交直线
分别交直线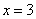 于点
于点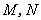 ,线段
,线段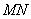 的中点为
的中点为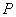 ,记直线
,记直线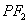 的斜率为
的斜率为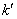 ,求证:
,求证: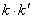 为定值.
为定值.
科目:高中数学 来源: 题型:
抛掷两颗质地均匀的骰子,计算:
(1)事件“两颗骰子点数相同”的概率;
(2)事件“点数之和小于7”的概率;
(3)事件“点数之和等于或大于11”的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两地相距1000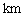 ,货车从甲地匀速
,货车从甲地匀速 行驶到乙地,速度不得超过80
行驶到乙地,速度不得超过80 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的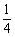 倍,固定成本为a元.
倍,固定成本为a元.
(1)将全程运输成本y(元)表示为速度v( )的函数,并指出这个函数的定义域;
)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,货车应以多大的速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法正确的是
A.“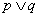 为真”是“
为真”是“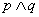 为真”的充分不必要条件;
为真”的充分不必要条件;
B.设有一个回归直线方程为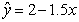 ,则变量
,则变量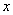 每增加一个单位,
每增加一个单位,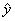 平均减少
平均减少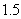 个单位;
个单位;
C.若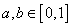 ,则不等式
,则不等式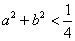 成立的概率是
成立的概率是 ;
;
D.已知空间直线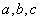 ,若
,若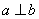 ,
,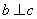 ,则
,则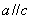 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
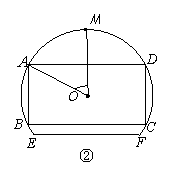
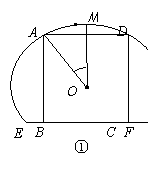
如图,一块弓形薄铁片EMF,点M为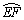 的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=
的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=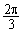 .将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗), AD∥EF,且点A、D在
.将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗), AD∥EF,且点A、D在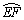 上,设∠AOD=
上,设∠AOD= .
.
(1)求矩形铁片ABCD的面积S关于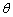 的函数关系式;
的函数关系式;
 (2)当矩形铁片ABCD的
(2)当矩形铁片ABCD的 面积最大时,求cos
面积最大时,求cos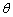 的值.
的值.
 |  | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com