
| A. | f(x)=x,g(x)=$\frac{{x}^{2}}{x}$ | B. | f(x)=x2,g(x)=($\sqrt{x}$)4 | C. | f(x)=x2,g(x)=$\root{3}{{x}^{6}}$ | D. | f(x)=1,g(x)=x0 |
分析 分别判断两个函数的定义域和对应法则是否相同即可.
解答 解:对于A,f(x)=x(x∈R),与g(x)=$\frac{{x}^{2}}{x}$=x(x≠0)的定义域不同,不是相等函数;
对于B,f(x)=x2(x∈R),与g(x)=${(\sqrt{x})}^{4}$=x2(x≥0)的定义域不同,不是相等函数;
对于C,f(x)=x2(x∈R),与g(x)=$\root{3}{{x}^{6}}$=x2(x∈R)的定义域相同,对应法则也相同,是相等函数;
对于D,f(x)=1(x∈R),与g(x)=x0=1(x≠0)的定义域不同,不是相等函数.
故选:C.
点评 本题考查了判断两个函数是否为相等函数的应用问题,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计).如果他在t4时刻卖出所有商品,那么他将获得的最大利润是( )
甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某人持有资金120万元,他可以在t1至t4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计).如果他在t4时刻卖出所有商品,那么他将获得的最大利润是( )| A. | 40万元 | B. | 60万元 | C. | 120万元 | D. | 140万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 0.88 | 1.30 | 1.406 | 1.431 | 1.52 | 1.62 | 1.70 | 1.875 | 2 |
| f(x) | -2 | -0.963 | -0.340 | -0.053 | 0.145 | 0.625 | 1.975 | 2.545 | 4.05 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
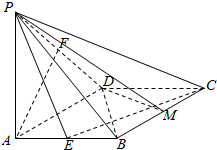 如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB、PD的中点.
如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB、PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com