Question

4．将边长为2的等边△ABC沿x轴正方向滚动，某时刻A与坐标原点重合（如图），设顶点A（x，y）的轨迹方程是y=f（x），关于函数y=f（x）有下列说法：
①f（x）的值域为[0，2]；
②f（x）是周期函数且周期为6；
③f（x）＜f（4）＜f（2015）；
④滚动后，当顶点A第一次落在x轴上时，的图象与x轴所围成的面积为$\frac{8π}{3}$+$\sqrt{3}$．
其中正确命题的序号为①②④．

Answer 1

分析 先根据题意画出顶点P（x，y）的轨迹，如图所示，它的轨迹是一段一段的圆弧组成的图形．从图形中可以看出，关于函数y=f（x）的说法的正确性．

解答 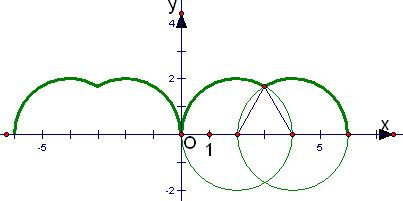解：根据题意画出顶点P（x，y）的轨迹，如图所示，
轨迹是一段一段的圆弧组成的图形．
从图形中可以看出，关于函数y=f（x）的有下列说法：
①f（x）的值域为[0，2]正确；
②f（x）是周期函数，周期为6，②正确；
③由于f（2015）=f（5）＜f（4），故③不正确；
④滚动后，当顶点A第一次落在x轴上时，的图象与x轴所围成的面积为
f（x）的图象在区间[0，6]上与x轴所围成的图形的面积，
其大小为一个正三角形和二段扇形的面积和，
其值为$\frac{1}{2}$×2×$\sqrt{3}$+2×（$\frac{1}{2}$×$\frac{2π}{3}$×2²）=$\sqrt{3}$+$\frac{8π}{3}$，故④正确，
故答案为：①②④．

点评 本小题主要考查命题的真假判断与应用、函数单调性的应用、函数奇偶性的应用等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想，属于中档题