Question

9．如图正方形ADMN与矩形ABCD所在平面互相垂直，点E在线段AB上，AB=2AD=6．
（Ⅰ）若AE=EB，求证：BM∥平面NDE；
（Ⅱ）若BE=2EA，求三棱锥M-DEN的体积．

Answer 1

分析 （I）连接AM，交ND于F，连接EF．由正方形性质可得AF=FM，又AE=EB，可得EF∥BM．利用线面平行的判定定理即可得出；
（II）当BE=2EA时，EA=$\frac{1}{3}$AB=2，利用线面垂直的判定定理可得：AB⊥平面ADMN．利用V_M-DEN=V_E-NDM=$\frac{1}{3}×AE×{S}_{△DNM}$，即可得出．

解答 （I）证明：连接AM，交ND于F，连接EF．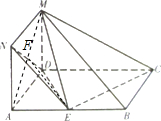
由正方形ADMN可得AF=FM，又AE=EB，
∴EF∥BM．
∵BM?平面NDE，EF?平面NDE，
∴BM∥平面NDE；
（II）解：当BE=2EA时，EA=$\frac{1}{3}$AB=2，
∵AB⊥AD，平面ADMN⊥平面ABCD，平面ADMN∩平面ABCD=AD，
∴AB⊥平面ADMN．
∴V_M-DEN=V_E-NDM=$\frac{1}{3}×AE×{S}_{△DNM}$=$\frac{1}{3}×2×\frac{1}{2}×{3}^{2}$=3．

点评 本题考查了正方形的性质、线面面面垂直与平行的判定与性质定理、三棱锥的体积计算公式、三角形中位线定理，考查了推理能力与计算能力，属于中档题．