
| A�� | $��\frac{��}{3}��\frac{2��}{3}��$ | B�� | $[\frac{��}{3}��\frac{2��}{3}]$ | C�� | $[0��\frac{��}{3}]��[\frac{2��}{3}���У�$D | D�� | $[0��\frac{��}{3}���ȣ�\frac{2��}{3}���У�$ |
���� ����Ҫ���ֱ��l�ķ��̣�����������l�Ƿ����б�ʣ�����б��ʱl���̱�Ϊy=kx+2�������������P��x��kx+2���������ܵõ�$\overrightarrow{PA}��\overrightarrow{PB}$�����꣬�Ӷ���������$\overrightarrow{PA}•\overrightarrow{PB}��0$��õ�����x�IJ���ʽ��1+k2��x2+4kx+3��0��Ҫ�����������ò���ʽ���н⣬�Ӷ�����0��������õ�k$��-\sqrt{3}����k��\sqrt{3}$���������������ʱl��б�Ǧ��ķ�Χ����������б��ʱ�������������Ƶķ��������жϳ�������������������Ӷ��õ�$��=\frac{��}{2}$������������Ħ������ɣ�
��� 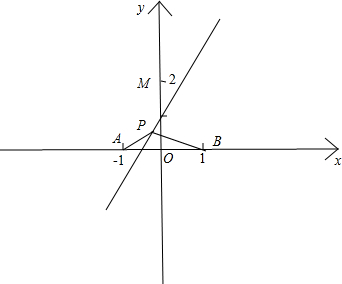 �⣺��ͼ��
�⣺��ͼ��
��1����l����б�ʣ���ֱ��l�ķ���Ϊy=kx+2��
����P��x��kx+2����
��$\overrightarrow{PA}•\overrightarrow{PB}$=��-1-x��-kx-2��•��1-x��-kx-2��=��1+k2��x2+4kx+3��0��
��ò���ʽ�н⣻
���=16k2-12��1+k2����0��
���k$��-\sqrt{3}$����k$��\sqrt{3}$��
��$tan����-\sqrt{3}����tan����\sqrt{3}$��
��$\frac{��}{3}������\frac{2��}{3}$����$����\frac{��}{2}$��
��2����l������б�ʣ���l����Ϊx=0��
����P��0��y����
��$\overrightarrow{PA}•\overrightarrow{PB}=��-1��-y��•��1��-y��={y}^{2}-1��0$��
��-1��y��1��
������P��ʹ$\overrightarrow{PA}•\overrightarrow{PB}��0$��
����ʱ$��=\frac{��}{2}$��
�����ϵ�ֱ��l����б�ǵķ�Χ��$��\frac{��}{3}��\frac{2��}{3}��$��
��ѡ��A��
���� ����ֱ�ߵĵ�бʽ���̣��ɵ�����������������꣬�������������������㣬һԪ���β���ʽ�Ƿ��н���б�ʽ���Ĺ�ϵ����Ϥ���к�����ͼ��֪����б�ǵ�ȡֵ��Χ��ע�ⲻҪ©��б�ʲ����ڵ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | l�ͦ���l�Φ� | B�� | l�Φ���l�Φ� | C�� | ���ͦã��áͦ� | D�� | ���Φã��áΦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{16}{3}$ | B�� | $\frac{8}{3}$ | C�� | $\frac{4}{3}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ADMN�����ABCD����ƽ�滥�ഹֱ����E���߶�AB�ϣ�AB=2AD=6��
��ͼ������ADMN�����ABCD����ƽ�滥�ഹֱ����E���߶�AB�ϣ�AB=2AD=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | -$\frac{3}{4}$ | C�� | $\frac{4}{3}$ | D�� | -$\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com