
 如图,AB为圆O的直径,直线CD与圆O相切于M,AD垂直CD于D,BC⊥CD于C,MN⊥AB于N,又AD=3,BC=1,则MN=$\sqrt{3}$.
如图,AB为圆O的直径,直线CD与圆O相切于M,AD垂直CD于D,BC⊥CD于C,MN⊥AB于N,又AD=3,BC=1,则MN=$\sqrt{3}$. 分析 连接AM,OM,BM,证明△CMB≌△NMB,可得CM=NM,再求出CD,即可求出MN.
解答  解:连接AM,OM,BM,则
解:连接AM,OM,BM,则
因为直线CD与圆O相切于M,
所以∠CMB=∠MAM,
因为AB为圆O的直径,MN⊥AB,
所以∠NMB=∠MAM,
所以∠CMB=∠NMB,
因为BC⊥CD于C,MN⊥AB,
所以△CMB≌△NMB,
所以CM=NM,
因为直线CD与圆O相切于M,AD垂直CD于D,BC⊥CD于C,AD=3,BC=1,
所以OM=2,
所以AB=4,
所以CD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
所以CM=$\sqrt{3}$
所以MN=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查三角形全等的证明,考查圆的切线的性质,属于中档题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
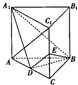 已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.
已知三棱柱ABC-A1B1C1中,AB=BC=BB1,AB⊥BC,BB1⊥平面ABC,D为AC的中点,E为CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将边长为2的等边△ABC沿x轴正方向滚动,某时刻A与坐标原点重合(如图),设顶点A(x,y)的轨迹方程是y=f(x),关于函数y=f(x)有下列说法:
将边长为2的等边△ABC沿x轴正方向滚动,某时刻A与坐标原点重合(如图),设顶点A(x,y)的轨迹方程是y=f(x),关于函数y=f(x)有下列说法:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | a>b>c | C. | a<c<b | D. | b>a>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com