
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
分析 由已知利用两角和的正弦函数公式,特殊角的三角函数值可求sinα+cosα=$\frac{\sqrt{6}}{2}$,两边平方,利用二倍角的正弦函数公式,诱导公式即可化简求值得解.
解答 解:∵$sin(\frac{π}{4}+α)=\frac{{\sqrt{3}}}{2}$=$\frac{\sqrt{2}}{2}$sinα+$\frac{\sqrt{2}}{2}$cosα,
∴sinα+cosα=$\frac{\sqrt{6}}{2}$,
∴两边平方可得:1+sin2α=$\frac{3}{2}$,解得:sin2α=$\frac{1}{2}$,
∴sin(-2α)=-sin2α=-$\frac{1}{2}$.
故选:B.
点评 本题主要考查了两角和的正弦函数公式,特殊角的三角函数值,二倍角的正弦函数公式,诱导公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{16\sqrt{3}}}{3}$ | B. | $16(2+\sqrt{3})$ | C. | $4(2-\sqrt{3})$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2+1 | B. | y=1-$\frac{1}{x}$ | C. | y=x2-5x-6 | D. | y=3-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
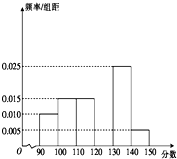 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如图所示的频率分布直方图,则估计本次考试的平均分为( )
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如图所示的频率分布直方图,则估计本次考试的平均分为( )| A. | 121 | B. | 119 | C. | 118.5 | D. | 118 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
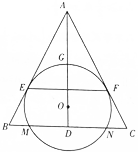 如图,O为等腰三角形ABC内一点,圆O与△ABC的底边BC交于M、N两点与底边上的高AD交于点G,与AB、AC分别相切于E、F两点.
如图,O为等腰三角形ABC内一点,圆O与△ABC的底边BC交于M、N两点与底边上的高AD交于点G,与AB、AC分别相切于E、F两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在(-∞,-1)上单调递增 | |
| B. | 函数f(x)在(-∞,-1)上单调递减 | |
| C. | 若b=0,则函数f(x)的图象与直线y=10只有一个公共点 | |
| D. | 若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com