
| a2b2 |
| a2+b2 |
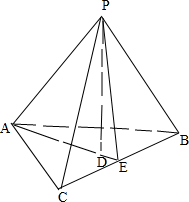 解:如图,设PA、PB、PC为三棱锥的三条两两互相垂直的侧棱,三棱锥P-ABC的高为PD=h,
解:如图,设PA、PB、PC为三棱锥的三条两两互相垂直的侧棱,三棱锥P-ABC的高为PD=h,| b2c2 |
| b2+c2 |
| PA2PE2 |
| PA2+PE2 |
a2•
| ||
a2+
|
| a2b2c2 |
| a2b2+b2c2+c2a2 |
| a2b2c2 |
| a2b2+b2c2+c2a2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
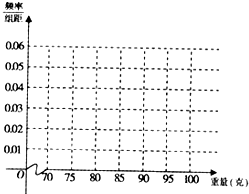 从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:
从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:| 分数(重量) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 30 | x | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
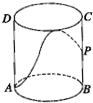 如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为4的正方形,P是BC中点,现有一只蚂蚁位于外壁外处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为
如图,有一圆柱形的开口容器(下表面密封),其轴截面是边长为4的正方形,P是BC中点,现有一只蚂蚁位于外壁外处,内壁P处有一米粒,则这只蚂蚁取得米粒所需经过的最短路程为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com