练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
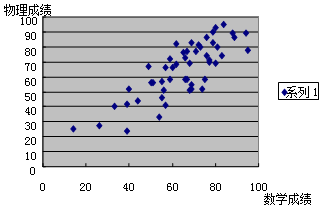
    16．在调查分析某班级数学成绩与物理成绩的相关关系时，对数据进行统计分析得到如下散点图，用回归直线$\hat y=bx+a$近似刻画其关系，根据图形，b的数值最有可能是（　　）
    A．0B．1.55C．0.45D．-0.24

    分析 从散点图来看某班级数学成绩与物理成绩的相关关系是正相关，回归直线的斜率不能是负值，又回归直线不和横轴平行，得到斜率不能是0，从散点图观察，直线应该比y=x的斜率要大一些，只有1.55符合题意，得到结果．

    解答 解：从散点图来看某班级数学成绩与物理成绩的相关关系是正相关，
    ∴回归直线的斜率不能是负值，
    ∴D不正确，
    ∵回归直线不和横轴平行，
    ∴斜率不能是0，
    ∴A不正确，
    从散点图观察，直线应该比y=x的斜率要大一些，只有1.55符合题意，
    故选B．

    点评 本题考查定性的分析回归直线，在一组具有相关关系的变量的数据（x与y）间，通过散点图可观察出所有数据点都分布在一条直线附近，通过散点图可以看出两个变量之间关系的大致情况．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．化简下列各式：
    （1）sin2αcos2α+cos4α+sin2α；
    （2）$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$（α为第二象限角）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．集合A={x∈N+|-1＜x＜4}，B={x|x2≤4}，则A∩B=（　　）
    A．{0，1，2}B．{1，2}C．{1，2，3}D．{0，1，2，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=$\sqrt{lo{g}_{2}x}$+$\sqrt{16-{4}^{x-1}}$．
    （1）求f（x）的定义域A；
    （2）若函数g（x）=x2+ax+b的零点为-1.5，当x∈A时，求函数g（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知θ∈（0，π），tanθ=-$\frac{3}{2}$，则cosθ=（　　）
    A．$\frac{3}{{\sqrt{13}}}$B．$-\frac{2}{{\sqrt{13}}}$C．$\frac{2}{{\sqrt{13}}}$D．$-\frac{3}{{\sqrt{13}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知一个圆锥的正视图和侧视图都是边长为1的正三角形，则它的俯视图的面积是（　　）
    A．πB．$\frac{π}{2}$C．$\frac{π}{3}$D．$\frac{π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知平面非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{b}$•（$\overrightarrow{a}+\overrightarrow{b}$）=1，且|$\overrightarrow{b}$|=1，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

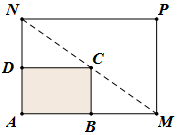    5．如图所示，某小区内有一矩形花坛，现将这一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求B点在AM上，D点在AN上，且对角线MN过C点，已知AB=3米，AD=2米．
    （Ⅰ）设DN=x米，BM=y米，矩形AMPN的面积为z米2，试用x，y表示z；
    （Ⅱ）当DN的长度是多少时，矩形花坛AMPN的面积最小？并求出最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知复数$z=\frac{2+i}{1-i}$（i为虚数单位），那么z的共轭复数为（　　）
    A．$\frac{3}{2}+\frac{3}{2}i$B．$\frac{1}{2}-\frac{3}{2}i$C．$\frac{1}{2}+\frac{3}{2}i$D．$\frac{3}{2}-\frac{3}{2}i$

    查看答案和解析>>

    同步练习册答案