
分析 根据条件求出an=f(2n)+1的表达式,利用等比数列的定义即可证明{an}为等比数列,即可求出通项公式.
解答 解:令n1=n2=1,得f(2)=1+f(1)+f(1),
则f(2)=3,a1=f(2)+1=4,
令n1=n2=2,得f(4)=1+f(2)+f(2),则f(4)=7,a2=f(4)+1=8,
令n1=n2=2n,得f(2n+2n)=1+f(2n)+f(2n),
即f(2n+1)=1+2f(2n),
则f(2n+1)+1=2[1+f(2n)],an+1=2an
所以,数列{an}是等比数列,公比q=2,首项a1=4.
所以an=4×2n-1=2n+1,
故答案为:2n+1
点评 本题主要考查等比数列的判断和证明,综合性较强,考查学生的计算能力.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 若直线l上有无数个点不在平面α内,则l∥α | |
| B. | 若直线l与平面α有两个公共点,则直线l在平面内 | |
| C. | 若直线l与平面α相交,则l与平面α内的任意直线都是异面直线 | |
| D. | 平行于同一个平面的两条直线平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
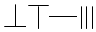 ,则9117用算筹可表示为( )
,则9117用算筹可表示为( )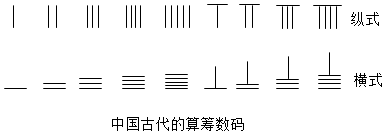
| A. | 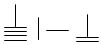 | B. | 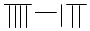 | C. |  | D. | 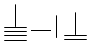 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
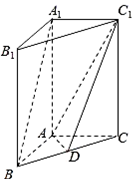 如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | e | C. | 3 | D. | 2e2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com