
【题目】已知函数![]() (a,
(a,![]() ).
).
(1)若![]() ,且
,且![]() 在
在![]() 内有且只有一个零点,求a的值;
内有且只有一个零点,求a的值;
(2)若![]() ,且
,且![]() 有三个不同零点,问是否存在实数a使得这三个零点成等差数列?若存在,求出a的值,若不存在,请说明理由;
有三个不同零点,问是否存在实数a使得这三个零点成等差数列?若存在,求出a的值,若不存在,请说明理由;
(3)若![]() ,
,![]() ,试讨论是否存在
,试讨论是否存在![]() ,使得
,使得![]() .
.
【答案】(1)![]() (2)存在;a的值为
(2)存在;a的值为![]() (3)答案不唯一,具体见解析
(3)答案不唯一,具体见解析
【解析】
(1)![]() ,
,![]() ,讨论
,讨论![]() 和
和![]() 两种情况,分别计算函数的单调性,再根据零点个数得到参数.
两种情况,分别计算函数的单调性,再根据零点个数得到参数.
(2)![]() ,根据题意
,根据题意![]() ,计算得到
,计算得到![]() ,
,![]() ,计算得到答案.
,计算得到答案.
(3)![]() ,
,![]() ,故必须
,故必须![]() 在
在![]() 上有解,解方程得到答案.
上有解,解方程得到答案.
(1)若![]() ,则
,则![]() ,
,![]() ,
,
若![]() ,则在
,则在![]() ,则
,则![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,故
,故![]() 在
在![]() 上无零点,舍;
上无零点,舍;
若![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
在![]() 上,
上,![]() ,
,![]() 在上单调递减,
在上单调递减,
在![]() 上,
上,![]() ,
,![]() 在上单调递增,
在上单调递增,
故![]() ,
,
若![]() ,则
,则![]() ,
,![]() 在
在![]() 上无零点,舍;
上无零点,舍;
若![]() ,则
,则![]() ,
,![]() 在
在![]() 上恰有一零点,此时
上恰有一零点,此时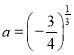 ;
;
若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
则![]() 在
在![]() 和
和![]() 上有各有一个零点,舍;
上有各有一个零点,舍;
故a的值为![]() .
.
(2)因为![]() ,则
,则![]() ,若
,若![]() 有三个不同零点,且成等差数列,可设
有三个不同零点,且成等差数列,可设![]() ,
,
故![]() ,则
,则![]() ,故
,故![]() ,
,![]() ,
,![]() .
.
此时,![]() ,
,![]() ,故存在三个不同的零点.
,故存在三个不同的零点.
故符合题意的a的值为![]() .
.
(3)若![]() ,
,![]() ,
,![]() ,
,
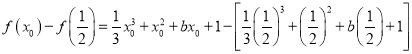

∴若存在![]() ,使得
,使得![]() ,
,
必须![]() 在
在![]() 上有解.
上有解.
![]() ,
,![]()
方程的两根为:![]() ,
,![]() ,
,
![]() 只能是
只能是![]() ,
,
依题意![]() ,即
,即![]() ,
,![]()
即![]() ,
,
又由![]() ,得
,得![]() ,故欲使满足题意的
,故欲使满足题意的![]() 存在,则
存在,则![]() ,
,
∴当![]() 时,存在唯一的
时,存在唯一的![]() 满足
满足![]() ,
,
当![]() 时,不存在
时,不存在![]() 使
使![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的偶函数,对于任意
上的偶函数,对于任意![]() ,都有
,都有![]() 成立,当
成立,当![]() ,且
,且![]() 时,都有
时,都有![]() ,给出下列命题,其中所有正确命题为( ).
,给出下列命题,其中所有正确命题为( ).
A.![]()
B.直线![]() 是函数
是函数![]() 的图象的一条对称轴
的图象的一条对称轴
C.函数![]() 在
在![]() 上为增函数
上为增函数
D.函数![]() 在
在![]() 上有四个零点
上有四个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,过点M(1,0)的直线l与抛物线C:y2=2px(p>0)交于A,B两点,且![]() .
.
(1)求抛物线C的方程;
(2)过点M作直线l'⊥l交抛物线C于两点,记△OAB,△OPQ的面积分别为S1,S2,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”.他把三角形的三条边分别称为小斜、中斜和大斜.三斜求积术就是用小斜平方加上大斜平方,送到中斜平方,取相减后余数的一半,自乘而得一个数,小斜平方乘以大斜平方,送到上面得到的那个数,相减后余数被4除,所得的数作为“实”,1作为“隅”,开平方后即得面积.所谓“实”、“隅”指的是在方程![]() 中,p为“隅”,q为“实”.即若
中,p为“隅”,q为“实”.即若![]() 的大斜、中斜、小斜分别为a,b,c,则
的大斜、中斜、小斜分别为a,b,c,则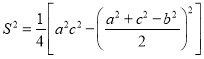 .已知点D是
.已知点D是![]() 边AB上一点,
边AB上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为
分别为![]() 的上、下顶点且
的上、下顶点且![]() 为
为![]() 外的动点,且
外的动点,且![]() 到
到![]() 上点的最近距离为1.
上点的最近距离为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,设直线
时,设直线![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,求
倍,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生社团对![]() 年元宵节当天游览磁器口古镇景区的游客满意度抽样调查,从当日
年元宵节当天游览磁器口古镇景区的游客满意度抽样调查,从当日![]() 万名游客中随机抽取
万名游客中随机抽取![]() 人进行统计,结果如下图的频率分布表和频率分布直方图:
人进行统计,结果如下图的频率分布表和频率分布直方图:
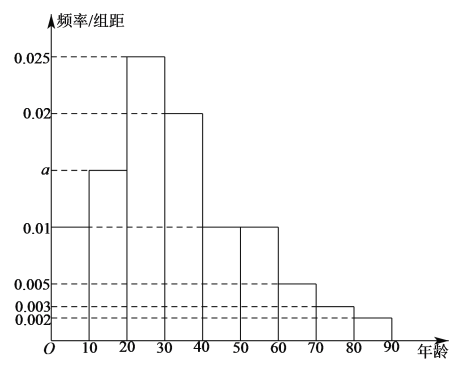
年龄 | 频数 | 频率 | 满意 | 不满意 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
|
|
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)利用频率分布直方图,估算游客的平均年龄和年龄的中位数;
(3)称年龄不低于![]() 岁的人群为“安逸人群”,完成
岁的人群为“安逸人群”,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为游客的满意度与“安逸人群”人数相关.
的把握认为游客的满意度与“安逸人群”人数相关.
|
| 合计 | |
满意 | |||
不满意 | |||
合计 |
参考公式: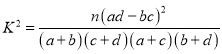 ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com