Question

10．执行如图所示的程序框图，则输出的y值为（　　）

• A． 1
• B． 0
• C． $\frac{\sqrt{3}}{2}$
• D． -$\frac{\sqrt{3}}{2}$

Answer 1

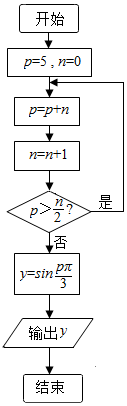
分析 模拟执行程序，依次写出每次循环得到的p，n的值，当p=-1时，不满足条件p＞$\frac{n}{2}$，退出循环，计算并输出y=sin（-$\frac{π}{3}$）=-$\frac{\sqrt{3}}{2}$，从而得解．

解答 解：模拟执行程序，可得
p=5，n=0
执行循环体，p=5，n=1
满足条件p＞$\frac{n}{2}$，执行循环体，p=4，n=2
满足条件p＞$\frac{n}{2}$，执行循环体，p=2，n=3
满足条件p＞$\frac{n}{2}$，执行循环体，p=-1，n=4
不满足条件p＞$\frac{n}{2}$，退出循环，y=sin（-$\frac{π}{3}$）=-$\frac{\sqrt{3}}{2}$，
输出y的值为-$\frac{\sqrt{3}}{2}$．
故选：D．

点评 本题主要考查了循环结构的程序框图和特殊角的三角函数值在三角函数求值中的应用，正确依次写出每次循环得到的p，n的值是解题的关键，属于基础题．