
分析 (1)由题意知$\left\{\begin{array}{l}{a<0}\\{a•(-\frac{1}{2a})^{2}-\frac{1}{2a}-a=\frac{17}{8}}\end{array}\right.$,从而解得;
(2)分类讨论,从而解不等式f(x)>1;
(3)分类讨论,从而分别判断一次函数与二次函数的性质并判断,从而求得.
解答 解:(1)∵函数f(x)有最大值$\frac{17}{8}$,
∴$\left\{\begin{array}{l}{a<0}\\{a•(-\frac{1}{2a})^{2}-\frac{1}{2a}-a=\frac{17}{8}}\end{array}\right.$,
解得,a=-2或a=-$\frac{1}{8}$;
(2)当a=0时,f(x)=x>1;
当a>0时,ax2+x-a>1,
即(x-1)(ax+a+1)>0;
故x>1或x<-$\frac{a+1}{a}$=-1-$\frac{1}{a}$;
当a<0时,ax2+x-a>1,
即a(x-1)(x+$\frac{a+1}{a}$)>0,
即(x-1)(x+$\frac{a+1}{a}$)<0;
当-1=$\frac{a+1}{a}$,即a=-$\frac{1}{2}$时,不等式无解;
当-$\frac{1}{2}$<a<0时,$\frac{a+1}{a}$<-1,
故1<x<-$\frac{a+1}{a}$;
当a<-$\frac{1}{2}$时,$\frac{a+1}{a}$>-1,
故-$\frac{a+1}{a}$<a<1;
(3)当a=0时,f(x)>0在x>1时恒成立;
当a≠0时,$\left\{\begin{array}{l}{a>0}\\{a+1-a≥0}\end{array}\right.$,
解得,a>0;
故a≥0.
点评 本题考查了函数的性质与不等式的关系应用及恒成立问题与最值问题的应用.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-2,2) | C. | (-1,5) | D. | (-2,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
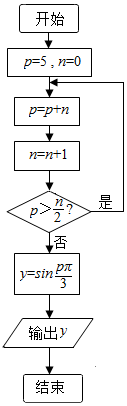
| A. | 1 | B. | 0 | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数 | [50,59) | [60,69) | [70,79) | [80,89) | [90,100] |
| 甲班频数 | 5 | 6 | 4 | 4 | 1 |
| 乙班频数 | 1 | 3 | 6 | 5 | 5 |
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com