
ЗжЮі ЃЈЂёЃЉгЩЬтвтПЩжЊЃЌ${S}_{n}=\frac{1}{3}{n}^{2}+\frac{2}{3}n$ЃЌЃЈnЁЪN*ЃЉЃЎгЩan=Sn-Sn-1ЧѓГіnЁн2ЪБЕФЭЈЯюЙЋЪНЃЌвбжЊn=1ГЩСЂЕУЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈЂђЃЉгЩbn=anan+1cos[ЃЈn+1ЃЉІа]=ЃЈ-1ЃЉn-1anan+1ЃЌЕУTn=b1+b2+Ё+bn=a1a2-a2a3+a3a4-a4a5+Ё+ЃЈ-1ЃЉn-1anan+1ЃЎНсКЯЃЈЂёЃЉЗжn=2mЃЈmЁЪN*ЃЉКЭn=2m-1ЃЈmЁЪN*ЃЉЧѓГіЪ§Са{bn}ЕФЧАnЯюКЭЮЊTnЃЌгЩTnЁнtn2ЖдnЁЪN*КуГЩСЂЃЌЗжРыВЮЪ§tПЩЕУЪЕЪ§tЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂѓЃЉгЩ${a_n}=\frac{2n+1}{3}$жЊЪ§Са{an}жаУПвЛЯюЖМВЛПЩФмЪЧХМЪ§ЃЎШчДцдквдa1ЮЊЪзЯюЃЌЙЋБШqЮЊ2Лђ4ЕФЪ§Са$\{{a_{n_k}}\}$ЃЈkЁЪN*ЃЉЃЌДЫЪБ{a${\;}_{{n}_{k}}$}жаУПвЛЯюГ§ЕквЛЯюЭтЖМЪЧХМЪ§ЃЌ
ЙЪВЛДцдквдa1ЮЊЪзЯюЃЌЙЋБШЮЊХМЪ§ЕФЪ§Са{a${\;}_{{n}_{k}}$}ЃЛЕБq=1ЪБЃЌЯдШЛВЛДцдкетбљЕФЪ§Са{a${\;}_{{n}_{k}}$}ЃЛЕБq=3ЪБЃЌШєДцдквдa1ЮЊЪзЯюЃЌЙЋБШЮЊ3ЕФЪ§Са{a${\;}_{{n}_{k}}$}ЃЈkЁЪN*ЃЉЃЌдђ${a}_{{n}_{1}}=1$ЃЈn1=1ЃЉЃЌгЩДЫПЩЕУ${a}_{{n}_{k}}={3}^{k-1}=\frac{2{n}_{k}+1}{3}$ЃЌ${n}_{k}=\frac{{3}^{k}-1}{2}$ЃЌМДДцдкТњзуЬѕМўЕФЪ§Са{a${\;}_{{n}_{k}}$}ЃЌЧв${n}_{k}=\frac{{3}^{k}-1}{2}$ЃЈkЁЪN*ЃЉЃЎ
НтД№ НтЃКЃЈЂёЃЉгЩЬтвтПЩжЊЃЌ${S}_{n}=\frac{1}{3}{n}^{2}+\frac{2}{3}n$ЃЌЃЈnЁЪN*ЃЉЃЎ
ЕБnЁн2ЪБЃЌ${a}_{n}={S}_{n}-{S}_{n-1}=\frac{1}{3}{n}^{2}+\frac{2}{3}n-$$[\frac{1}{3}ЃЈn-1ЃЉ^{2}+\frac{2}{3}ЃЈn-1ЃЉ]$=$\frac{2n+1}{3}$ЃЛ
ЕБn=1ЪБЃЌa1=S1=1ЪЪКЯЩЯЪНЃЎ
Ъ§Са{an}ЕФЭЈЯюЙЋЪНЮЊ${a}_{n}=\frac{2n+1}{3}$ЃЈnЁЪN*ЃЉЃЛ
ЃЈЂђЃЉЁпbn=anan+1cos[ЃЈn+1ЃЉІа]=ЃЈ-1ЃЉn-1anan+1ЃЌ
ЁрTn=b1+b2+Ё+bn=a1a2-a2a3+a3a4-a4a5+Ё+ЃЈ-1ЃЉn-1anan+1ЃЎ
гЩЃЈЂёЃЉПЩжЊЃЌЪ§Са{an}ЪЧвд1ЮЊЪзЯюЃЌЙЋВюЮЊ$\frac{2}{3}$ЕФЕШВюЪ§СаЃЎ
ЂйЕБn=2mЃЈmЁЪN*ЃЉЪБЃЌ${T_n}={T_{2m}}={a_1}{a_2}-{a_2}{a_3}+{a_3}{a_4}-{a_4}{a_5}+Ё+{ЃЈ-1ЃЉ^{2m-1}}{a_{2m}}{a_{2m+1}}$
=a2ЃЈa1-a3ЃЉ+a4ЃЈa3-a5ЃЉ+Ё+a2mЃЈa2m-1-a2m+1ЃЉ=$-\frac{4}{3}ЃЈ{a_2}+{a_4}+Ё+{a_{2m}}ЃЉ=-\frac{4}{3}ЁС\frac{{{a_2}+{a_{2m}}}}{2}ЁСm$
=$-\frac{1}{9}ЃЈ8{m^2}+12mЃЉ=-\frac{1}{9}ЃЈ2{n^2}+6nЃЉ$ЃЛ
ЂкЕБn=2m-1ЃЈmЁЪN*ЃЉЪБЃЌ${T_n}={T_{2m-1}}={T_{2m}}-{ЃЈ-1ЃЉ^{2m-1}}{a_{2m}}{a_{2m+1}}$
=$-\frac{1}{9}ЃЈ8{m^2}+12mЃЉ+\frac{1}{9}ЃЈ16{m^2}+16m+3ЃЉ$=$\frac{1}{9}ЃЈ8{m^2}+4m+3ЃЉ=\frac{1}{9}ЃЈ2{n^2}+6n+7ЃЉ$ЃЎ
Ёр${T_n}=\left\{\begin{array}{l}-\frac{1}{9}ЃЈ2{n^2}+6nЃЉЃЌnЮЊХМЪ§\\ \frac{1}{9}ЃЈ2{n^2}+6n+7ЃЉЃЌnЮЊЦцЪ§\end{array}\right.$ЃЎ
вЊЪЙTnЁнtn2ЖдnЁЪN*КуГЩСЂЃЌжЛвЊЪЙ$-\frac{1}{9}ЃЈ2{n^2}+6nЃЉЁнt{n^2}$ЃЈnЮЊе§ХМЪ§ЃЉКуГЩСЂЃЌМДЪЙ$-\frac{1}{9}ЃЈ2+\frac{6}{n}ЃЉЁнt$ЖдnЮЊе§ХМЪ§КуГЩСЂЃЌ
Ёрt$Ём-\frac{5}{9}$ЃЎ
ЙЪЪЕЪ§tЕФШЁжЕЗЖЮЇЪЧ$ЃЈ-ЁоЃЌ-\frac{5}{9}]$ЃЛ
ЃЈЂѓЃЉгЩ${a_n}=\frac{2n+1}{3}$жЊЪ§Са{an}жаУПвЛЯюЖМВЛПЩФмЪЧХМЪ§ЃЎ
ЂйШчДцдквдa1ЮЊЪзЯюЃЌЙЋБШqЮЊ2Лђ4ЕФЪ§Са$\{{a_{n_k}}\}$ЃЈkЁЪN*ЃЉЃЌДЫЪБ{a${\;}_{{n}_{k}}$}жаУПвЛЯюГ§ЕквЛЯюЭтЖМЪЧХМЪ§ЃЌ
ЙЪВЛДцдквдa1ЮЊЪзЯюЃЌЙЋБШЮЊХМЪ§ЕФЪ§Са{a${\;}_{{n}_{k}}$}ЃЛ
ЂкЕБq=1ЪБЃЌЯдШЛВЛДцдкетбљЕФЪ§Са{a${\;}_{{n}_{k}}$}ЃЛЕБq=3ЪБЃЌШєДцдквдa1ЮЊЪзЯюЃЌЙЋБШЮЊ3ЕФЪ§Са{a${\;}_{{n}_{k}}$}ЃЈkЁЪN*ЃЉЃЌдђ${a}_{{n}_{1}}=1$ЃЈn1=1ЃЉЃЌ
${a}_{{n}_{k}}={3}^{k-1}=\frac{2{n}_{k}+1}{3}$ЃЌ${n}_{k}=\frac{{3}^{k}-1}{2}$ЃЌМДДцдкТњзуЬѕМўЕФЪ§Са{a${\;}_{{n}_{k}}$}ЃЌЧв${n}_{k}=\frac{{3}^{k}-1}{2}$ЃЈkЁЪN*ЃЉЃЎ
ЕуЦР БОЬтжївЊПМВщЪ§СаКЭКЏЪ§ЕФгІгУЃЌИљОнЬѕМўЭЦГіЪ§СаЕФЕнЭЦЙиЯЕЪЧНтОіБОЬтЕФЙиМќЃЎПМВщЪ§СаЕФЗжРрЧѓКЭЃЌПМВщТпМЫМЮЌФмСІгыЭЦРэдЫЫуФмСІЃЌзлКЯадНЯЧПЃЌФбЖШНЯДѓЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт

| AЃЎ | 20Іа | BЃЎ | 16Іа | CЃЎ | 15Іа | DЃЎ | 12Іа |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
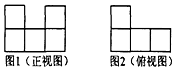 гУШєИЩИіРтГЄЮЊ1cmЕФаЁе§ЗНЬхЕўГЩвЛИіМИКЮЬхЃЌЭМ1ЮЊЦфе§ЪгЭМЃЌЭМ2ЮЊЦфИЉЪгЭМЃЌШєетИіМИКЮЬхЕФЬхЛ§ЮЊ7cm3ЃЌдђЦфВрЪгЭМЮЊЃЈЁЁЁЁЃЉ
гУШєИЩИіРтГЄЮЊ1cmЕФаЁе§ЗНЬхЕўГЩвЛИіМИКЮЬхЃЌЭМ1ЮЊЦфе§ЪгЭМЃЌЭМ2ЮЊЦфИЉЪгЭМЃЌШєетИіМИКЮЬхЕФЬхЛ§ЮЊ7cm3ЃЌдђЦфВрЪгЭМЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 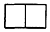 | BЃЎ | 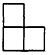 | CЃЎ |  | DЃЎ |  |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЂйЂм | BЃЎ | ЂкЂл | CЃЎ | ЂйЂл | DЃЎ | ЂкЂм |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈ-$\frac{1}{3}$ЃЌ+ЁоЃЉ | BЃЎ | ЃЈ-$\frac{1}{3}$ЃЌ1ЃЉ | CЃЎ | ЃЈ-$\frac{1}{3}$ЃЌ$\frac{1}{3}$ЃЉ | DЃЎ | ЃЈ-ЁоЃЌ-$\frac{1}{3}$ЃЉ |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com