
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| x+1 |
| x2-1 |
| A、(-∞,1] |
| B、(-1,0)∪[1,+∞) |
| C、(-∞,0)∪[1,+∞) |
| D、(-∞,0]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、若l∥α,m∥α,则l∥m |
| B、若l∥α,l∥β,则α∥β |
| C、若l∥m,l⊥α,则m⊥α |
| D、若l∥α,α⊥β,则l⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、l个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
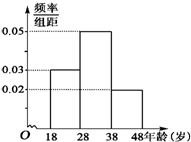 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:| 组数 | 分组 | 回答正确的人数 | 占本组的频率 |
| 第1组 | [18,28) | 240 | x |
| 第2组 | [28,38) | 300 | 0.6 |
| 第3组 | [38,48] | a | 0.4 |
| t-40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com