
| A. | ($\frac{1}{2}$,1)∪(1,+∞) | B. | (0,$\frac{1}{2}$)∪(1,+∞) | C. | ($\frac{1}{2}$,1)∪(1,2) | D. | (0,$\frac{1}{2}$)∪(1,2) |
分析 设f(x)=a|x|,g(x)=x2-$\frac{1}{2}$,根据不等式的大小关系转化为两个函数的图象关系,利用分类讨论以及数形结合进行求解即可.
解答 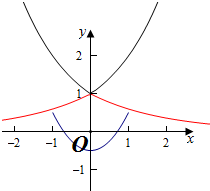 解:设f(x)=a|x|,g(x)=x2-$\frac{1}{2}$,
解:设f(x)=a|x|,g(x)=x2-$\frac{1}{2}$,
当x∈[-1,1]时,g(x)∈[-$\frac{1}{2}$,$\frac{1}{2}$],
∵f(x)和g(x)都是偶函数,
∴只要保证当x∈[0,1]时,不等式a|x|>x2-$\frac{1}{2}$恒成立即可.
当x∈[0,1]时,f(x)=ax,
若a>1时,f(x)=ax≥1,此时不等式a|x|>x2-$\frac{1}{2}$恒成立,满足条件.
若0<a<1时,f(x)=ax为减函数,而g(x)为增函数,
此时要使不等式a|x|>x2-$\frac{1}{2}$恒成立,则只需要f(1)>g(1)即可,
即a>1-$\frac{1}{2}$=$\frac{1}{2}$,
此时$\frac{1}{2}$<a<1,
综上$\frac{1}{2}$<a<1或a>1,
故选:A.
点评 本题主要考查不等式恒成立问题,根据条件构造函数,转化为两个函数的函数值的大小关系,利用数形结合是解决本题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 角α为第二象限角 | B. | α=$\frac{360°}{π}$ | C. | sinα>0 | D. | sinα<cosα |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
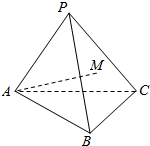 如图,在三棱锥P-ABC中,AB=AC=PB=PC=10,PA=8,BC=12,点M在平面PBC内,且AM=7,设异面直线AM与BC所成角为α,则cosα的最大值为( )
如图,在三棱锥P-ABC中,AB=AC=PB=PC=10,PA=8,BC=12,点M在平面PBC内,且AM=7,设异面直线AM与BC所成角为α,则cosα的最大值为( )| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{6}{7}$ | D. | $\frac{4\sqrt{3}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com