
【题目】已知圆 ![]() ,圆心为
,圆心为 ![]() ,定点
,定点 ![]() ,
, ![]() 为圆
为圆 ![]() 上一点,线段
上一点,线段 ![]() 上一点
上一点 ![]() 满足
满足 ![]() ,直线
,直线 ![]() 上一点
上一点 ![]() ,满足
,满足 ![]() .
.
(Ⅰ)求点 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(Ⅱ) ![]() 为坐标原点,
为坐标原点, ![]() 是以
是以 ![]() 为直径的圆,直线
为直径的圆,直线 ![]() 与
与 ![]() 相切,并与轨迹
相切,并与轨迹 ![]() 交于不同的两点
交于不同的两点 ![]() .当
.当 ![]() 且满足
且满足 ![]() 时,求
时,求 ![]() 面积
面积 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)∵ ![]()
∴ ![]() 为线段
为线段 ![]() 中点
中点
∵ ![]()
∴ ![]() 为线段
为线段 ![]() 的中垂线
的中垂线
∴ ![]()
∵ ![]()
∴由椭圆的定义可知 ![]() 的轨迹是以
的轨迹是以 ![]() 为焦点,长轴长为
为焦点,长轴长为 ![]() 的椭圆,
的椭圆,
设椭圆的标准方程为 ![]() ,
,
则 ![]() ,
, ![]() ,
,
∴ ![]() 。
。
∴点 ![]() 的轨迹
的轨迹 ![]() 的方程为
的方程为 ![]() 。
。
(Ⅱ)∵圆 ![]() 与直线
与直线 ![]() 相切,
相切,
∴ ![]() ,即
,即 ![]() ,
,
由 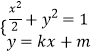 ,消去
,消去 ![]() .
.
∵直线 ![]() 与椭圆交于两个不同点,
与椭圆交于两个不同点,
∴ ![]() ,
,
将 ![]() 代入上式,可得
代入上式,可得 ![]() ,
,
设 ![]() ,
, ![]() ,
,
则 ![]() ,
, ![]() ,
,
∴ ![]()
![]() ,
,
∴ ![]()
∴ ![]() ,
,
∵ ![]() ,解得
,解得 ![]() .满足
.满足 ![]() 。
。
又 ![]() ,
,
设 ![]() ,则
,则 ![]() .
.
∴ ![]()
![]() ,
,
∴ ![]()
故 ![]() 面积
面积 ![]() 的取值范围为
的取值范围为 ![]() 。
。
【解析】(1)根据题意易得QN为线段![]() 的中垂线,可得
的中垂线,可得![]() ,所以
,所以![]() ,由椭圆的定义可知Q的轨迹是以
,由椭圆的定义可知Q的轨迹是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆。
的椭圆。
(2)由直线 l : y = k x + m 与 ⊙ O 相切可得![]() =1即
=1即![]() 。将该式与Q的轨迹C的方程联立整理后得
。将该式与Q的轨迹C的方程联立整理后得![]() ,可以表示出
,可以表示出![]()
![]() ,又直线 l 与椭圆交于两个不同点,根据题目中λ的范围和这个条件可求出k的范围。
,又直线 l 与椭圆交于两个不同点,根据题目中λ的范围和这个条件可求出k的范围。![]() ,根据求出的k的范围即可求出S的取值范围。
,根据求出的k的范围即可求出S的取值范围。


科目:高中数学 来源: 题型:
【题目】已知△ABC的角A,B,C所对的边分别为a,b,c,设向量![]() =(a,b),
=(a,b),![]() =(sin B,sin A),
=(sin B,sin A), ![]() =(b-2,a-2).
=(b-2,a-2).
(1)若![]() ∥
∥![]() ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形;
(2)若![]() ⊥
⊥![]() ,边长c=2,∠C=
,边长c=2,∠C=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且在
,且在![]() 上是增函数;
上是增函数;
定义行列式![]() ; 函数
; 函数![]() (其中
(其中![]() ).
).
(1) 证明: 函数![]() 在
在![]() 上也是增函数;
上也是增函数;
(2) 若函数![]() 的最大值为4,求
的最大值为4,求![]() 的值;
的值;
(3) 若记集合M={m|恒有g(![]() )<0},
)<0},![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:ax+ ![]() y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D.给出下列命题:p:a>0,S△AOB=
y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D.给出下列命题:p:a>0,S△AOB= ![]() ,q:a>0,|AB|<|CD|.则下面命题正确的是( )
,q:a>0,|AB|<|CD|.则下面命题正确的是( )
A.p∧q
B.¬p∧¬q
C.p∧¬q
D.¬p∧q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com