
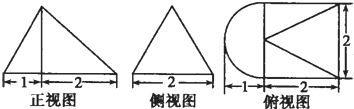
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
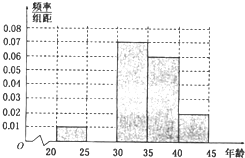 在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,据此估计这800名志愿者年龄在[25,30)的人数为
在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,据此估计这800名志愿者年龄在[25,30)的人数为查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 5 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、62 | B、105 |
| C、168 | D、231. |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
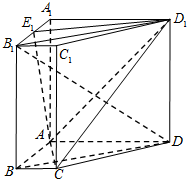 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com