
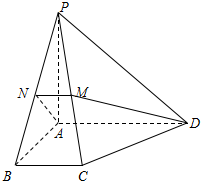
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠BAD=90°,PA=AB,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠BAD=90°,PA=AB,M,N分别为PC,PB的中点.分析 (1)欲证MN∥平面PAD,根据线面平行的判定定理知,只须证明MN∥AD,结合中点条件即可证明得;
(2)欲证PN⊥平面ADMN,根据线面垂直的性质定理,只须证明AN⊥PN及AD⊥PN,而这此垂直关系的证明较为明显,从而即可证得结论.
解答  证明:(1)因为M、N分别为PC、PB的中点,
证明:(1)因为M、N分别为PC、PB的中点,
所以MN∥BC,…(1分)
又因为AD∥BC,所以MN∥AD…(2分)
又AD?平面PAD,MN?平面PAD,
所以MN∥平面PAD…(4分)
(2)因为AN为等腰△ABP底边PB上的中线,所以AN⊥PN…(5分)
因为PA⊥平面ABCD,AD?平面ABCD,所以AD⊥PA.
又因为AD⊥AB,且AB∩AP=A,所以AD⊥平面PAB.
又PN?平面PAB,所以AD⊥PN…(6分)
因为AN⊥PN,AD⊥PN,且AN∩AD=A,
所以PN⊥平面ADMN…(7分)
点评 本小题主要考查直线与平面平行的判定、直线与平面垂直的性质,考查了运算求解能力,考查了空间想象力及推理论证能力,属于中档题.


科目:高中数学 来源: 题型:填空题
 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
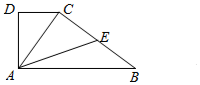 如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=3,AD=$\sqrt{2}$,E为BC中点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3,则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3.
如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=3,AD=$\sqrt{2}$,E为BC中点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3,则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
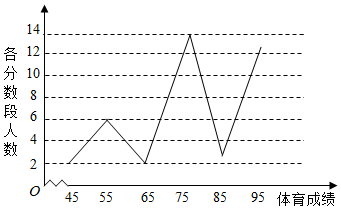 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com