
| A. | $\frac{16}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{3}{4}$ |
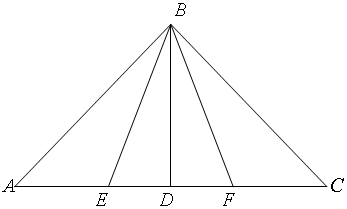
分析 由题意,设AC=6,点E,F是斜边AC的三等分点,可得EF=2.过B点作AC的垂下交于D,利用三角函数的定义可得tan∠DBF的值,利用二倍角可得答案.
解答 解:由题意,设AC=6,点E,F是斜边AC的三等分点,可得EF=2.过B点作AC的垂下交于D,∠DBF=∠DBE.
∵△ABC是等腰直角三角形,
∴ AB=BC=$2\sqrt{3}$.DC=3
AB=BC=$2\sqrt{3}$.DC=3
由勾股定理,可得:DB=3.
那么:tan∠DBF=$\frac{1}{3}$.
∴tan∠EBF=tan2∠DBF=$\frac{2tan∠DBF}{1-ta{n}^{2}∠DBF}$=$\frac{3}{4}$.
故选:D.
点评 本题考查了三角函数的定义的运用和等腰直角三角形的性质.属于基础题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,4] | B. | [$\frac{3-\sqrt{5}}{2}$,4] | C. | [3-$\sqrt{5}$,2] | D. | [$\frac{3-\sqrt{5}}{2}$,3-$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{2}$ | C. | $\frac{1}{π}$ | D. | $-\frac{1}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $k<\frac{2}{5}$ | B. | $k≤\frac{2}{5}$ | C. | $0<k≤\frac{2}{5}$ | D. | $0≤k≤\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 结论正确 | B. | 大前提错误 | C. | 小前提错误 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com