
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{2}$ | C. | $\frac{1}{π}$ | D. | $-\frac{1}{π}$ |
分析 求出函数的导数,可得切线的斜率,由两直线平行的条件:斜率相等,解方程可得a的值.
解答 解:y=axcosx的导数为y′=a(cosx-xsinx),
可得在x=$\frac{π}{2}$处的切线斜率为a(cos$\frac{π}{2}$-$\frac{π}{2}$sin$\frac{π}{2}$)=-$\frac{π}{2}$a,
由切线的斜率为$\frac{1}{2}$,
可得-$\frac{π}{2}$a=$\frac{1}{2}$,
解得a=-$\frac{1}{π}$,
故选:D.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,正确求导和运用两直线平行的条件是解题的关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | -1 | 2 | 4 |
| P | $\frac{1}{5}$ | $\frac{2}{3}$ | p1 |
| A. | 0 | B. | $\frac{2}{15}$ | C. | $\frac{1}{15}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}+\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}+\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
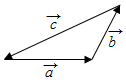
| A. | $\overrightarrow a+\overrightarrow b=\overrightarrow c$ | B. | $\overrightarrow a+\overrightarrow b=-\overrightarrow c$ | C. | $\overrightarrow a-\overrightarrow b=-\overrightarrow c$ | D. | $\overrightarrow b+\overrightarrow c=\overrightarrow a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数 | 6 | 14 | 18 | 27 | 20 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com