
| A. | [2,4] | B. | [$\frac{3-\sqrt{5}}{2}$,4] | C. | [3-$\sqrt{5}$,2] | D. | [$\frac{3-\sqrt{5}}{2}$,3-$\sqrt{5}$] |
分析 先建立坐标系,根据$\overrightarrow{PB}$•$\overrightarrow{PC}$=1,得到点P在x2+y2=2的圆周上,即P在$\widehat{MN}$上,将P的坐标范围表示出来,进而可求$\overrightarrow{AP}$•$\overrightarrow{AB}$.
解答 解:以BC中点O为原点,BC所在的直线为x轴,建立如图所示的坐标系,
∵正三角形ABC边长为2,
∴B(-1,0),A(0,$\sqrt{3}$),C(1,0),
设P的坐标为(x,y),
∴$\overrightarrow{PB}$=(-1-x,-y),$\overrightarrow{PC}$=(1-x,-y),
∴$\overrightarrow{PB}$•$\overrightarrow{PC}$=x2-1+y2=1,
即点P在x2+y2=2的圆弧即$\widehat{MN}$上,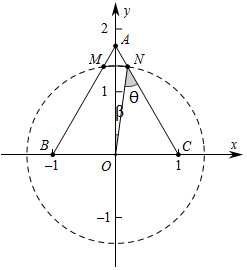
如图可以求出sinθ=$\frac{\sqrt{6}}{4}$,cosθ=$\frac{\sqrt{10}}{4}$;
β=θ-$\frac{π}{6}$,sinβ=$\frac{3\sqrt{2}-\sqrt{10}}{8}$,cosβ=$\frac{\sqrt{30}+\sqrt{6}}{8}$,
设∠AOP=φ,则-β≤φ≤β,P($\sqrt{2}$sinφ,$\sqrt{2}$cosφ),
$\overrightarrow{AP}$=($\sqrt{2}$sinφ,$\sqrt{2}$cosφ-$\sqrt{3}$),
又$\overrightarrow{AB}$=(-1,-$\sqrt{3}$),
所以$\overrightarrow{AP}$•$\overrightarrow{AB}$=-$\sqrt{2}$sinφ-$\sqrt{6}$cosφ+3,-β≤φ≤β,
当φ=-β时,$\overrightarrow{AP}$•$\overrightarrow{AB}$最大,$\overrightarrow{AP}$•$\overrightarrow{AB}$=(-$\sqrt{2}$)×(-$\frac{3\sqrt{2}-\sqrt{10}}{8}$)-$\sqrt{6}$×$\frac{\sqrt{30}+\sqrt{6}}{8}$+3=3-$\sqrt{5}$;
当φ=β时,$\overrightarrow{AP}$•$\overrightarrow{AB}$最小,$\overrightarrow{AP}$•$\overrightarrow{AB}$=(-$\sqrt{2}$)×$\frac{3\sqrt{2}-\sqrt{10}}{8}$-$\sqrt{6}$×$\frac{\sqrt{30}+\sqrt{6}}{8}$+3=$\frac{3-\sqrt{5}}{2}$;
所以$\overrightarrow{AP}$•$\overrightarrow{AB}$的范围是[$\frac{3-\sqrt{5}}{2}$,3-$\sqrt{5}$].
故本题选D.
点评 本题考查了数量积运算,直线和圆的位置关系,培养了学生的运算能力和转化能力,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{11}{21}$ | C. | $\frac{10}{21}$ | D. | $\frac{5}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{5π}{12}$个单位 | D. | 向右平移$\frac{5π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| ξ | -1 | 2 | 4 |
| P | $\frac{1}{5}$ | $\frac{2}{3}$ | p1 |
| A. | 0 | B. | $\frac{2}{15}$ | C. | $\frac{1}{15}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
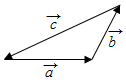
| A. | $\overrightarrow a+\overrightarrow b=\overrightarrow c$ | B. | $\overrightarrow a+\overrightarrow b=-\overrightarrow c$ | C. | $\overrightarrow a-\overrightarrow b=-\overrightarrow c$ | D. | $\overrightarrow b+\overrightarrow c=\overrightarrow a$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1296种 | B. | 216种 | C. | 864种 | D. | 1080种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com