
���� ��1������$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}\right.$���ѵ�P�ļ����껯Ϊֱ�����꣬����Բ�ķ��̻�Ϊֱ�����귽�̣������жϳ�λ�ù�ϵ��
��2����1����Ϊ��Q������C�ϣ��ʿ����Q������Ϊ$��cos����\sqrt{3}sin����$���Ӷ���Q��ֱ��l�ľ���Ϊ $d=\frac{{|cos��+\sqrt{3}sin��-8|}}{{\sqrt{1+1}}}$���������������Ǻ����ĵ����Լ��ɵó���
��2��ֱ��l��ƽ����n���̿���Ϊ��x+y+t=0������Բ����������Ϊ 4x2+2tx+t2-3=0�����á�=0�������õ㵽ֱ�ߵľ��빫ʽ���ɵó���
��� �⣺��1�����P��ֱ������ϵ����Ϊ��x0��y0������$\left\{\begin{array}{l}{x_0}=4\sqrt{2}cos\frac{��}{4}=4\\{y_0}=4\sqrt{2}sin\frac{��}{4}=4\end{array}\right.$���ã�P��4��4���� ��
$\left\{\begin{array}{l}x=cos��\\ y=\sqrt{3}sin��\end{array}\right.����Ϊ������⇒\frac{x^2}{1}+\frac{y^2}{3}={cos^2}��+si{n^2}��=1$��
��$\frac{4^2}{1}+\frac{4^2}{3}��1$��
���P������C ${x^2}+\frac{y^2}{3}=1$�⣮
��2����1����Ϊ��Q������C�ϣ��ʿ����Q������Ϊ$��cos����\sqrt{3}sin����$��
�Ӷ���Q��ֱ��l�ľ���Ϊ $d=\frac{{|cos��+\sqrt{3}sin��-8|}}{{\sqrt{1+1}}}$=$\frac{{8-2cos����-\frac{��}{3}��}}{{\sqrt{2}}}=4\sqrt{2}-\sqrt{2}cos����-\frac{��}{3}��$��
��$cos����-\frac{��}{3}��=1$ʱ��Q��ֱ��l�ľ���d����СֵΪ$3\sqrt{2}$��
��$cos����-\frac{��}{3}��=-1$ʱ��Q��ֱ��l�ľ���d�����ֵΪ$5\sqrt{2}$��
��2��ֱ��l��ƽ����n���̿���Ϊ��x+y+t=0��
����$\left\{\begin{array}{l}{x^2}+\frac{y^2}{3}=1\\ x+y+t=0\end{array}\right.$�� 3x2+��x+t��2=3���� 4x2+2tx+t2-3=0��
��=4t2-16��t2-3��=-12t2+48=0⇒t=��2��
����C�������߷���Ϊ x+y+2=0��x+y-2=0��
Q��ֱ��l�ľ���d�����ֵΪ $d=\frac{|2-��-8��|}{{\sqrt{1+1}}}=5\sqrt{2}$��
Q��ֱ��l�ľ���d����СֵΪ $d=\frac{|-2-��-8��|}{{\sqrt{1+1}}}=3\sqrt{2}$��
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡��㵽ֱ�ߵľ��빫ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M⊆N | B�� | N⊆M | ||
| C�� | M=N | D�� | M��N֮��û�а�����ϵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
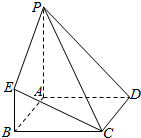 ����ͼ��ʾ�ļ������У��ı���ABCDΪ�����Σ�PA��ƽ��ABCD��PA��BE��AB=PA=6��BE=3��
����ͼ��ʾ�ļ������У��ı���ABCDΪ�����Σ�PA��ƽ��ABCD��PA��BE��AB=PA=6��BE=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | $\frac{1}{2}$ | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 8�� | C�� | 12�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=0 | B�� | f��x��=2 | C�� | f��x��=x2-1 | D�� | f��x��=x-$\frac{1}{x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com