
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由函数y=$\frac{sinx}{x}$≤1,和两角和差的正弦公式得到2(A-B)>sin(A-B)恒成立,
解答 解:由2A-sinAcosB>2B-cosAsinB,得2(A-B)>sin(A-B),
由于y=$\frac{sinx}{x}$≤1,
∴2(A-B)>sin(A-B)恒成立,
∴由“A>B“一定能推出“2A-sinAcosB>2B-cosAsinB“,
但是“2A-sinAcosB>2B-cosAsinB“推不出A>B“,
故A>B“是“2A-sinAcosB>2B-cosAsinB“充分不必要条件,
故选:A.
点评 本题考查了充分必要条件,关键是掌握函数y=$\frac{sinx}{x}$≤1,属于中档题.


科目:高中数学 来源: 题型:选择题
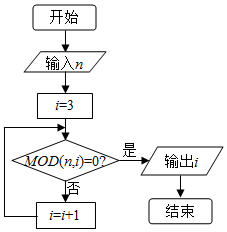 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
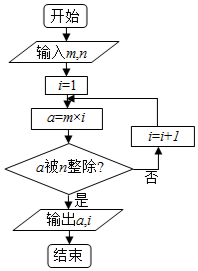 当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )
当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )| A. | 37${C}_{12}^{7}$ | B. | 38${C}_{12}^{8}$ | C. | -33${C}_{12}^{3}$ | D. | -37${C}_{12}^{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x-1+1(x>2) | B. | y=2x+1+1(x>0) | C. | y=2x-1-1(x>2) | D. | y=2x+1-1(x>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2|x| | B. | f(x)=-xe|x| | ||
| C. | f(x)=$\left\{\begin{array}{l}{lg(x+1),x≥0}\\{lg(1-x),x<0}\\{\;}\end{array}\right.$ | D. | f(x)=x+sinx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com