
分析 由题意知an+an+1=cn,anan+1=($\frac{1}{3}$)n,从而可得$\frac{{a}_{n+2}}{{a}_{n}}$=$\frac{1}{3}$,从而写出an=$\left\{\begin{array}{l}{2•(\frac{1}{3})^{\frac{n-1}{2}},n为奇数}\\{\frac{1}{6}•(\frac{1}{3})^{\frac{n-2}{2}},n为偶数}\end{array}\right.$,讨论n以求Sn,最后以分段形式写出即可.
解答 解:∵an,an+1是方程x2-cnx+($\frac{1}{3}$)n=0的两根,
∴an+an+1=cn,anan+1=($\frac{1}{3}$)n,
∵anan+1=($\frac{1}{3}$)n,an+1an+2=($\frac{1}{3}$)n+1,
∴$\frac{{a}_{n+2}}{{a}_{n}}$=$\frac{1}{3}$,
故数列{an}的奇数项成等比数列,公比为$\frac{1}{3}$,偶数项成等比数列,公比为$\frac{1}{3}$;
可知a1=2,a2=$\frac{1}{6}$;
故an=$\left\{\begin{array}{l}{2•(\frac{1}{3})^{\frac{n-1}{2}},n为奇数}\\{\frac{1}{6}•(\frac{1}{3})^{\frac{n-2}{2}},n为偶数}\end{array}\right.$,
当n为奇数时,
Sn=c1+c2+c3+…+cn
=(a1+a2)+(a2+a3)+…+(an-1+an)+(an+an+1)
=2(a1+a2+a3+…+an-1+an+an+1)-(an+1+a1)
=2($\frac{2(1-(\frac{1}{3})^{\frac{n+1}{2}})}{1-\frac{1}{3}}$+$\frac{\frac{1}{6}(1-(\frac{1}{3})^{\frac{n+1}{2}})}{1-\frac{1}{3}}$)-(2+$\frac{1}{2}$•($\frac{1}{3}$)${\;}^{\frac{n+1}{2}}$)
=4$\frac{1}{2}$-7•($\frac{1}{3}$)${\;}^{\frac{n+1}{2}}$;
当n为偶数时,
Sn=Sn-1+cn=4$\frac{1}{2}$-7•($\frac{1}{3}$)${\;}^{\frac{n}{2}}$+an+an+1
=4$\frac{1}{2}$-7•($\frac{1}{3}$)${\;}^{\frac{n}{2}}$+$\frac{1}{2}$•($\frac{1}{3}$)${\;}^{\frac{n}{2}}$+2($\frac{1}{3}$)${\;}^{\frac{n}{2}}$
=4$\frac{1}{2}$(1-($\frac{1}{3}$)${\;}^{\frac{n}{2}}$).
综上所述,
Sn=$\left\{\begin{array}{l}{4\frac{1}{2}-7•\frac{1}{{3}^{\frac{n+1}{2}}},n为奇数}\\{4\frac{1}{2}(1-\frac{1}{{3}^{\frac{n}{2}}}),n为偶数}\end{array}\right.$.
点评 本题考查了学生的化简能力分类讨论的思想应用,同时考查了构造法的应用.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:选择题
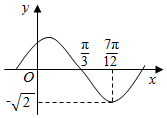 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则$f(\frac{11π}{24})$的值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则$f(\frac{11π}{24})$的值为( )| A. | $-\frac{{\sqrt{6}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{16}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
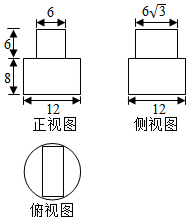 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 360π+108$\sqrt{3}$ | B. | 288π+180$\sqrt{3}$ | C. | 288π+216$\sqrt{3}$ | D. | 360π+156$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com