Question

2．若M为△ABC的重心，O为任意一点，$\overrightarrow{OA}$$+\overrightarrow{OB}$$+\overrightarrow{OC}$=n$\overrightarrow{OM}$，则n=（　　）

• A． 0
• B． 1
• C． 2
• D． 3

Answer 1

分析 可作出图形，从而有$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM}$，M为重心，从而有$\overrightarrow{AM}=\frac{1}{3}（\overrightarrow{AB}+\overrightarrow{AC}）$，再根据向量减法的几何意义便可以得到$n\overrightarrow{OM}=\frac{n}{3}（\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}）$，这样根据平面向量基本定理便可得到$\frac{n}{3}=1$，从而便可得出n的值．

解答 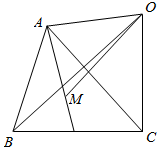解：如图，
$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM}$=$\overrightarrow{OA}+\frac{2}{3}[\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）]$=$\overrightarrow{OA}+\frac{1}{3}[（\overrightarrow{OB}-\overrightarrow{OA}）+（\overrightarrow{OC}-\overrightarrow{OA}）]$=$\frac{1}{3}（\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}）$；
∴$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=n\overrightarrow{OM}=\frac{n}{3}（\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}）$；
∴$\frac{n}{3}=1$；
∴n=3．
故选D．

点评 考查向量加法、减法及数乘的几何意义，向量加法的平行四边形法则，以及平面向量基本定理．