
分析 由点Pn与Qn的坐标关系得到数列递推式,两边取对数可得数列{$lg\frac{{a}_{n}}{2}$}构成以$lg\frac{1}{4}=-2lg2$为首项,以$\frac{1}{3}$为公比的等比数列,求得等比数列的通项公式后由对数的运算性质可得数列{an}的通项.
解答 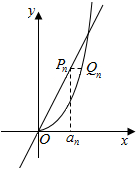 解:由题意可知,a1=$\frac{1}{2}$,
解:由题意可知,a1=$\frac{1}{2}$,
Pn的横坐标为an,纵坐标为2an,则Qn的纵坐标为2an,
∴Qn的横坐标为$\root{3}{4{a}_{n}}$,即${a}_{n+1}=\root{3}{4{a}_{n}}$,
∴${{a}_{n+1}}^{3}=4{a}_{n}$,
两边取对数得:3lgan+1=lgan+2lg2,
即$lg{a}_{n+1}=\frac{1}{3}lg{a}_{n}+\frac{2}{3}lg2$,化为$lg{a}_{n+1}-lg2=\frac{1}{3}(lg{a}_{n}-lg2)$,
即$lg\frac{{a}_{n+1}}{2}=\frac{1}{3}lg\frac{{a}_{n}}{2}$,
∴数列{$lg\frac{{a}_{n}}{2}$}构成以$lg\frac{1}{4}=-2lg2$为首项,以$\frac{1}{3}$为公比的等比数列,
∴$lg\frac{{a}_{n}}{2}=-2(\frac{1}{3})^{n-1}lg2$=$lg{2}^{-2(\frac{1}{3})^{n-1}}$,
则$\frac{{a}_{n}}{2}={2}^{-2(\frac{1}{3})^{n-1}}$,
∴${a}_{n}={2}^{1-2(\frac{1}{3})^{n-1}}$.
点评 本题考查数列递推式,考查等比关系的确定,由题意求得数列递推式是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{7}$) | B. | ($\frac{2}{7}$,$\frac{2}{3}$) | C. | ($\frac{2}{3}$,$\frac{4}{5}$) | D. | ($\frac{2}{7}$,$\frac{4}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
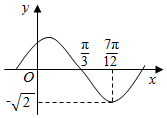 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则$f(\frac{11π}{24})$的值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则$f(\frac{11π}{24})$的值为( )| A. | $-\frac{{\sqrt{6}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,x${\;}_{0}^{2}≠1$ | B. | ?x0∈R,x${\;}_{0}^{2}>1$ | C. | ?x∈R,x2=1 | D. | ?x∈R,x2≠1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{16}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com