练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设x，y满足约束条件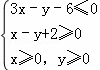，若目标函数z=ax+by（a＞0，b＞0）的最大值为12，则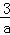+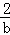的最小值为（　　）

    　

    A．

    4

    B．

    C．

    1

    D．

    2


    A.

    【解析】作出不等式组表示的平面区域，

    得到如图的四边形OABC及其内部，其中

    A（2，0），B（4，6），C（0，2），O为坐标原点

    设z=F（x，y）=ax+by（a＞0，b＞0），将直线l：z=ax+by进行平移，

    观察y轴上的截距变化，可得当l经过点B时，目标函数z达到最大值

    ∴z最大值=F（4，6）=12，即4a+6b=12．

    因此，+=（+）×（4a+6b）=2+（），

    ∵a＞0，b＞0，可得≥=12，

    ∴当且仅当即2a=3b=3时，的最小值为12，

    相应地，+=2+（）有最小值为4．

    故选：A


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    随机变量X的分布列为

    X

    x1

    x2

    x3

    P

    p1

    p2

    p3

    若p1，p2，p3成等差数列，则公差d的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有10件不同工厂生产的同类产品．

    (1)在商品评选会上，有2件商品不能参加评选，要选出4件商品，并排定选出的4件商品的名次，有多少种不同的选法？

    (2)若要选6件商品放在不同的位置上陈列，且必须将获金质奖章的两件商品放上，有多少种不同的布置方法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知P为三角形ABC内部任一点（不包括边界），且满足(-)·(+-2)=0，则DABC的形状一定为___________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    运行右面框图输出的S是254，则①应为

    (A) ≤5    (B) ≤6    (C)≤7    (D) ≤8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3＋x，对任意的m∈[－2,2]，f(mx－2)＋f(x)<0恒成立，则x的取值范围为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将圆x2+y2=4上各点的纵坐标压缩至原来的，所得曲线记作C；将直线3x﹣2y﹣8=0绕原点逆时针旋转90°所得直线记作l．

    （I）求直线l与曲线C的方程；

    （II）求C上的点到直线l的最大距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设不等式组表示的平面区域为M，不等式组表示的平面区域为N．在M内随机取一个点，这个点在N内的概率的最大值是________________.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知F是双曲线（a＞0，b＞0）的左焦点，E是该双曲线的右顶点，过点F且垂直于x轴的直线与双曲线交于A、B两点，点在以为直径的圆内，则该双曲线的离心率e的取值范围为（    ）

      A．（1，＋∞）   B．（1，2）        C．（1，1＋）   D．

    查看答案和解析>>

    同步练习册答案