
(2014•揭阳三模)已知函数f(x)是定义在R上的奇函数,且当x∈(﹣∞,0]时,f(x)=e﹣x﹣ex2+a,则函数f(x)在x=1处的切线方程为( )
A.x+y=0 B.ex﹣y+1﹣e=0 C.ex+y﹣1﹣e=0 D.x﹣y=0
B
【解析】
试题分析:利用f(0)=0先求出a的值,设x∈(0,+∞),根据已知条件求出f(﹣x),再利用奇函数,求出f(x)在(0,+∞)上的解析式,同时可求出导函数;求出切点坐标,再求出该点处的导数即为切线的斜率,利用点斜式表示出直线方程即可.
【解析】
由题意得,f(0)=1﹣0+a=0,解得a=﹣1,
∴当x∈(﹣∞,0]时,f(x)=e﹣x﹣ex2﹣1,
设x∈(0,+∞),则﹣x<0,f(﹣x)=ex﹣ex2﹣1,
∵f(x)是定义在R上的奇函数,
∴f(x)=﹣f(﹣x)=﹣ex+ex2+1,此时x∈(0,+∞),
∴f′(x)=﹣ex+2ex,
∴f′(1)=e,
把x=1代入f(x)=﹣ex+ex2+1得,f(1)=1,则切点为(1,1),
∴所求的切线方程为:y﹣1=e(x﹣1),化简得ex﹣y﹣e+1=0,
故选B.


科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.2排序不等式练习卷(解析版) 题型:解答题
已知a,b,c为正数,用排序不等式证明:2(a3+b3+c3)≥a2(b+c)+b2(a+c)+c2(a+b).
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.3绝对值不等式的解法练习卷(解析版) 题型:选择题
(2014•宜春模拟)若关于x的不等式|x﹣1|+|x﹣3|≤a2﹣2a﹣1在R上的解集为∅,则实数a的取值范围是( )
A.a<﹣1或a>3 B.a<0或a>3 C.﹣1<a<3 D.﹣1≤a≤3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.2基本不等式练习卷(解析版) 题型:选择题
(2014•咸阳二模)若正实数a,b满足a+b=1,则( )
A.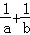 有最大值4 B.ab有最小值
有最大值4 B.ab有最小值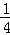
C.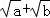 有最大值
有最大值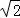 D.a2+b2有最小值
D.a2+b2有最小值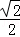
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷(解析版) 题型:选择题
(2014•安徽模拟)直线x﹣3y﹣1=0的倾斜角为α,曲线y=lnx在(x0,lnx0)处的切线的倾斜角为2α,则x0的值是( )
A.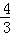 B.
B. C.
C.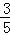 D.
D.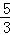
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷(解析版) 题型:选择题
(2014•郴州三模)在平面直角坐标系xOy中,已知P是函数f(x)=xlnx﹣x的图象上的动点,该曲线在点P处的切线l交y轴于点M(0,yM),过点P作l的垂线交y轴于点N(0,yN).则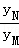 的范围是( )
的范围是( )
A.(﹣∞,﹣1]∪[3,+∞) B.(﹣∞,﹣3]∪[1,+∞)
C.[3,+∞) D.(﹣∞,﹣3]
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷(解析版) 题型:选择题
(2014•江西三模)已知函数f(x)=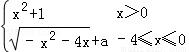 在点(1,2)处的切线与f(x)的图象有三个公共点,则a的取值范围是( )
在点(1,2)处的切线与f(x)的图象有三个公共点,则a的取值范围是( )
A.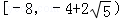 B.
B.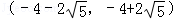
C.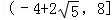 D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修1-2 4.2结构图练习卷(解析版) 题型:选择题
如图是《集合》的知识结构图,如果要加入“子集”,那么应该放在( )

A.“集合”的下位 B.“含义与表示”的下位
C.“基本关系”的下位 D.“基本运算”的下位
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-7 1.4分数法练习卷(解析版) 题型:选择题
(2011•张家界模拟)在调试某设备的线路设计中,要选一个电阻,调试者手中只有阻值分别为0.9KΩ,1.1KΩ,2.7KΩ,3KΩ,3.6KΩ,4KΩ,5KΩ等七种阻值不等的定值电阻,他用分数法进行优选试验时,依次将电阻值从小到大安排序号,则第1个试点的阻值是( )
A.1.1KΩ B.2.7KΩ C.3.6KΩ D.5KΩ
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com