
分析 (1)利用向量基本线性运算与基本定理化简;
(2)利用公式$|\overrightarrow{a}|\\;=\\;\sqrt{{\overrightarrow{a}}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}}$来计算向量模长;
(3)重心性质知:$\overrightarrow{AO}+\overrightarrow{DO}+\overrightarrow{MO}=\overrightarrow 0$,所以有(x+y-1)$\overrightarrow{AO}$+(-x)$\overrightarrow{DO}$+(-y)$\overrightarrow{AO}$=$\overrightarrow{0}$;
解答 解: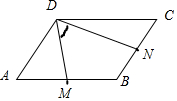 (I)如右图所示,
(I)如右图所示,
$\overrightarrow{DM}$=$\overrightarrow{DA}$+$\overrightarrow{AM}$
=$\frac{1}{2}\overrightarrow{AB}$-$\overrightarrow{AD}$;
$\overrightarrow{DN}$=$\overrightarrow{DC}$+$\overrightarrow{CN}$
=$;\overrightarrow{AB}$$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{CB}$=$\overrightarrow{AB}$-$\frac{1}{2}\overrightarrow{AD}$;
(II)由(I)知$\overrightarrow{AD}=\frac{2}{3}\overrightarrow{DN}-\frac{4}{3}\overrightarrow{DM},\overrightarrow{AB}=\frac{4}{3}\overrightarrow{DN}-\frac{2}{3}\overrightarrow{DM}$;
所以$|{\overrightarrow{AD}}|=\sqrt{{{({\frac{2}{3}\overrightarrow{DN}-\frac{4}{3}\overrightarrow{DM}})}^2}}=\frac{4}{3},|{\overrightarrow{AB}}|=\sqrt{{{({\frac{4}{3}\overrightarrow{DN}-\frac{2}{3}\overrightarrow{DM}})}^2}}=\frac{2}{3}\sqrt{13}$;
(III)由重心性质知:$\overrightarrow{AO}+\overrightarrow{DO}+\overrightarrow{MO}=\overrightarrow 0$,所以有:
$\begin{array}{l}\overrightarrow 0=x\overrightarrow{AD}+y\overrightarrow{AM}-\overrightarrow{OA}=x({\overrightarrow{AO}-\overrightarrow{DO}})+y({\overrightarrow{AO}-\overrightarrow{MO}})-\overrightarrow{AO}\\=({x+y-1})\overrightarrow{AO}+({-x})\overrightarrow{DO}+({-y})\overrightarrow{MO}\end{array}$
所以$({x+y-1}):({-x}):({-y})=1:1:1⇒x=y=\frac{1}{3}$;
点评 本题主要考查了向量的基本线性运算,向量模长求法以及三角形重心性质等知识点,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{9}{10}π,-\frac{3}{10}π]$ | B. | $[\frac{2}{5}π,\frac{9}{10}π]$ | C. | $[\frac{π}{10},\frac{π}{4}]$ | D. | $[-π,-\frac{π}{10}]∪(\frac{π}{4},π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5) | B. | (2,2) | C. | (1,3) | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲组 | 乙组 | 合计 | |
| 男生 | 7 | 6 | |
| 女生 | 5 | 12 | |
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
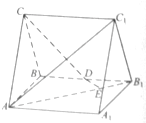 如图,直三棱柱ABC-A1B1C1中,AC=BC,AA1=AB,D为BB1的中点,E为AB1上的一点,AE=3EB1.
如图,直三棱柱ABC-A1B1C1中,AC=BC,AA1=AB,D为BB1的中点,E为AB1上的一点,AE=3EB1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com