
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.
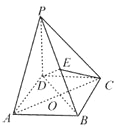
(1)求证![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用线面垂直的性质得![]() ,利用菱形的性质得
,利用菱形的性质得![]() ,利用线面垂直的判定定理得
,利用线面垂直的判定定理得![]() 平面
平面![]() ,利用线面垂直得到线线垂直,从而得到
,利用线面垂直得到线线垂直,从而得到![]() ;
;
(2)分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,设
轴的正方向建立空间直角坐标系,设![]() ,用坐标表示点,求得平面
,用坐标表示点,求得平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为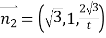 ,根据二面角
,根据二面角![]() 的余弦值为
的余弦值为![]() ,可求出
,可求出![]() ,从而得到点
,从而得到点![]() 的坐标,再利用向量的夹角公式,即可求得
的坐标,再利用向量的夹角公式,即可求得![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)∵![]() 平面
平面![]() ,∴
,∴![]()
又∵四边形![]() 为菱形,∴
为菱形,∴![]()
又![]() ,∴
,∴![]() 平面
平面![]()
![]() 平面
平面![]() ,∴
,∴![]()
(2)连![]() ,在
,在![]() 中,
中,![]() ,∴
,∴![]() 平面
平面![]()
分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系.
轴的正方向建立空间直角坐标系.
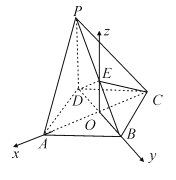
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
由(1)知,平面![]() 的一个法向量为
的一个法向量为![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则由
,则由
即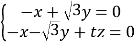 ,令
,令![]() ,则
,则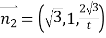
因二面角![]() 的余弦值为
的余弦值为![]() ,
,
∴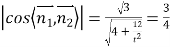 ,∴
,∴![]()
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,∵
,∵![]() ,
,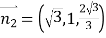 ,
,
∴ .
.


科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)=a![]() (a为常数).
(a为常数).
(1)求a的值;
(2)若函数g(x)=|(2x+1)f(x)|﹣k有2个零点,求实数k的取值范围;
(3)若x∈[﹣2,﹣1]时,不等式f(x)![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
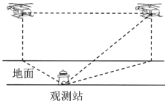
【题目】2019年10月1日,在庆祝新中国成立70周年阅兵中,由我国自主研制的军用飞机和军用无人机等参阅航空装备分秒不差飞越天安门,壮军威,振民心,令世人瞩目.飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析.一次飞行训练中,地面观测站观测到一架参阅直升飞机以![]() 千米/小时的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西
千米/小时的速度在同一高度向正东飞行,如图,第一次观测到该飞机在北偏西![]() 的方向上,1分钟后第二次观测到该飞机在北偏东
的方向上,1分钟后第二次观测到该飞机在北偏东![]() 的方向上,仰角为
的方向上,仰角为![]() ,则直升机飞行的高度为________千米.(结果保留根号)
,则直升机飞行的高度为________千米.(结果保留根号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将曲线![]() 上每个点的横坐标伸长为原来的
上每个点的横坐标伸长为原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A.![]() 的图象关于直线
的图象关于直线![]() 对称
对称
B.![]() 在
在![]() 上的值域为
上的值域为![]()
C.![]() 的图象关于点
的图象关于点![]() 对称
对称
D.![]() 的图象可由
的图象可由![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的离心率正好是双曲线
的离心率正好是双曲线![]() 的离心率的倒数,椭圆
的离心率的倒数,椭圆![]() 的短轴长等于抛物线
的短轴长等于抛物线![]() 上一点
上一点![]() 到抛物线焦点
到抛物线焦点![]() 的距离.
的距离.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 的两个交点为
的两个交点为![]() ,
,![]() 两点,已知圆
两点,已知圆![]() :
:![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() (点
(点![]() 在
在![]() 轴的正半轴),且直线
轴的正半轴),且直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的面积与
的面积与![]() 的面积乘积的最大值.
的面积乘积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术·均输》中有如下问题:“今有五人分十钱,令上二人所得与下三人等,问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分10钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
A.![]() 钱B.
钱B.![]() 钱C.
钱C.![]() 钱D.
钱D.![]() 钱
钱
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com