
【题目】已知椭圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的离心率正好是双曲线
的离心率正好是双曲线![]() 的离心率的倒数,椭圆
的离心率的倒数,椭圆![]() 的短轴长等于抛物线
的短轴长等于抛物线![]() 上一点
上一点![]() 到抛物线焦点
到抛物线焦点![]() 的距离.
的距离.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 的两个交点为
的两个交点为![]() ,
,![]() 两点,已知圆
两点,已知圆![]() :
:![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() (点
(点![]() 在
在![]() 轴的正半轴),且直线
轴的正半轴),且直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的面积与
的面积与![]() 的面积乘积的最大值.
的面积乘积的最大值.
【答案】(1)![]() (2)12
(2)12
【解析】
(1)根据题意分别写出椭圆的离心率,短轴长,从而得到关于![]() 的方程组,解出
的方程组,解出![]() 的值,得到椭圆方程;(2)根据直线与圆相切,得到
的值,得到椭圆方程;(2)根据直线与圆相切,得到![]() 的关系
的关系![]() ,分别表示出点
,分别表示出点![]() 、
、![]() 到直线
到直线![]() 的距离,直线与椭圆联立,得到
的距离,直线与椭圆联立,得到![]() ,
,![]() ,从而表示出
,从而表示出![]() ,然后表示出
,然后表示出![]() ,代入
,代入![]() 的关系,利用基本不等式,求出最大值.
的关系,利用基本不等式,求出最大值.
解:(1)双曲线![]() 的离心率为
的离心率为![]()
所以椭圆![]() 的离心率
的离心率![]() ,
,
抛物线![]() 的准线为
的准线为![]() ,
,
所以抛物线![]() 上一点
上一点![]() 到抛物线焦点
到抛物线焦点![]() 的距离为
的距离为![]() ,
,
所以椭圆![]() 的短轴长为
的短轴长为![]() ,则
,则![]()
设椭圆![]() 的焦距为
的焦距为![]() ,
,
所以得到,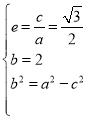 ,解得
,解得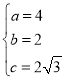 ,
,
因此,椭圆![]() 的方程为
的方程为![]() .
.
(2)由题意知,直线![]() 的斜率存在且斜率不为零,不妨设直线
的斜率存在且斜率不为零,不妨设直线![]() 的方程为
的方程为![]() ,
,
设点![]() ,
,![]() ,
,
由于直线![]() 与圆
与圆![]() 相切,则有
相切,则有![]() ,所以
,所以![]() .
.
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立
的方程联立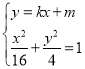 ,
,
消去![]() 并整理得
并整理得![]() .
.
由韦达定理可得![]() ,
,![]() .
.
记![]() 的面积为
的面积为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,
由弦长公式可得![]()
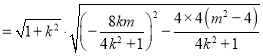
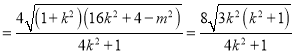 .
.
所以,![]()
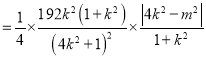
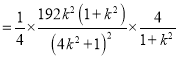
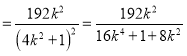
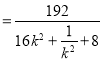
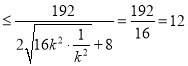 .
.
当且仅当![]() 时,即当
时,即当![]() 时,等号成立.
时,等号成立.
因此,![]() 的最大值为12.
的最大值为12.


科目:高中数学 来源: 题型:
【题目】在数列的每相邻两项之间插入此两项的和,形成新的数列,这样的操作叫做该数列的一次拓展.如数列1,2,经过第1次拓展得到数列1,3,2;经过第2次拓展得到数列1,4,3,5,2;设数列a,b,c经过第n次拓展后所得数列的项数记为![]() ,所有项的和记为
,所有项的和记为![]() .
.
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)若![]() ,求n的最小值;
,求n的最小值;
(3)是否存在实数a,b,c,使得数列![]() 为等比数列,若存在,求a,b,c满足的条件;若不存在,请说明理由.
为等比数列,若存在,求a,b,c满足的条件;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.
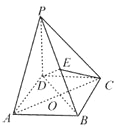
(1)求证![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同零点,是否存在实数
的两个不同零点,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数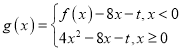 ,存在
,存在![]() 个零点.
个零点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设![]() 分别是这
分别是这![]() 个零点中的最小值与最大值,求
个零点中的最小值与最大值,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且此抛物线的准线被椭圆
的焦点重合,且此抛物线的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,试问直线
的垂直平分线,试问直线![]() 是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点为
的左右焦点为![]() 为它的中心,
为它的中心,![]() 为双曲线右支上的一点,
为双曲线右支上的一点,![]() 的内切圆圆心为
的内切圆圆心为![]() ,且圆
,且圆![]() 与
与![]() 轴相切于
轴相切于![]() 点,过
点,过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若双曲线的离心率为
,若双曲线的离心率为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 与
与![]() 关系不确定
关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在![]() 内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
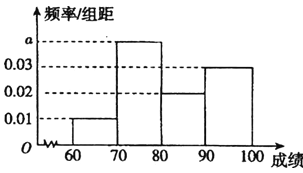
(1)已知成绩合格的200名参赛选手成绩的频率分布直方图如图,求a的值及估计这200名参赛选手的成绩平均数;
(2)根据已有的经验,参加复活赛的选手能够进入第二轮比赛的概率为![]() ,假设每名选手能否通过复活赛相互独立,现有3名选手进入复活赛,记这3名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.
,假设每名选手能否通过复活赛相互独立,现有3名选手进入复活赛,记这3名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com