
分析 (1)根据三角恒等变换化简f(x),得到f(x)=sin(ωx+$\frac{π}{4}$),结合函数的周期性求出ω的值即可;
(2)求出函数f(x)在区间$[-\frac{π}{4},\frac{π}{2}]$上的单调性,从而求出函数的最大值和最小值即可.
解答 解:(1)$f(x)=sin\frac{ωx}{2}cos(\frac{ωx}{2}+\frac{π}{4})-cos\frac{ωx}{2}sin(\frac{ωx}{2}-\frac{π}{4})$
=$\frac{\sqrt{2}}{2}$(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$-sin2$\frac{ωx}{2}$)-$\frac{\sqrt{2}}{2}$(cos$\frac{ωx}{2}$sin$\frac{ωx}{2}$-cos2$\frac{ωx}{2}$)
=$\frac{\sqrt{2}}{2}$(cos2$\frac{ωx}{2}$-sin2$\frac{ωx}{2}$)
=$\frac{\sqrt{2}}{2}$cosωx,
∵最小正周期T=$\frac{2π}{ω}$=π,∴ω=2.
(2)f(x)=$\frac{\sqrt{2}}{2}$cos2x,
x∈$[-\frac{π}{4},\frac{π}{2}]$,2x∈[-$\frac{π}{2}$,π],
f(x)在[-$\frac{π}{4}$,0]上是增函数,在[0,$\frac{π}{2}$]是减函数,
f(-$\frac{π}{4}$)=0,f(0)=$\frac{\sqrt{2}}{2}$,f($\frac{π}{2}$)=-$\frac{\sqrt{2}}{2}$,
故函数f(x)在区间[-$\frac{π}{4}$,$\frac{π}{2}$]上的最大值为$\frac{\sqrt{2}}{2}$,最小值为-$\frac{\sqrt{2}}{2}$.
点评 本题考查了三角函数的化简问题,考查三角函数的性质,是一道中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
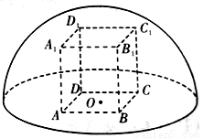
如图所示,直四棱柱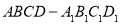 内接于半径为
内接于半径为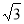 的半球
的半球 ,四边形
,四边形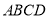 为正方形,则该四棱柱的体积最大时,
为正方形,则该四棱柱的体积最大时,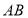 的长为( )
的长为( )
A. B.
B.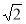 C.
C.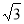 D.
D.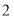
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 2 | 8 | 15 | 15 | 4 | 6 |
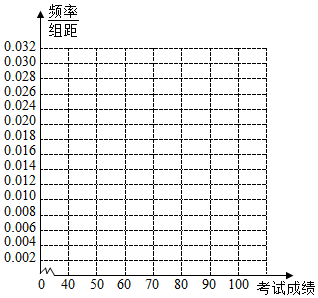
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
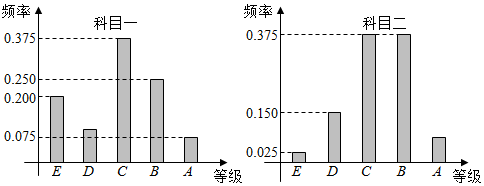
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{9}$ | D. | $\frac{3}{20}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com