
【题目】已知函数![]() 的定义域是A,值域是
的定义域是A,值域是![]() ;
;![]() 的定义域是C,值域是
的定义域是C,值域是![]() ,且实数
,且实数![]() 满足
满足![]() .下列命题中,正确的有( )
.下列命题中,正确的有( )
A.如果对任意![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
B.如果对任意![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
C.如果存在![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
D.如果存在![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() .
.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 为直线
为直线![]() 上的动点,
上的动点,![]() ,过
,过![]() 作直线
作直线![]() 的垂线
的垂线![]() ,
,![]() 交
交![]() 的中垂线于点
的中垂线于点![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于![]() 四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
(1)求恰有1人申请![]() 片区房源的概率;
片区房源的概率;
(2)用![]() 表示选择
表示选择![]() 片区的人数,求
片区的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在矩形![]() 中,
中,![]() ,沿直线BD将△ABD折成
,沿直线BD将△ABD折成![]() ,使得点
,使得点![]() 在平面
在平面![]() 上的射影在
上的射影在![]() 内(不含边界),设二面角
内(不含边界),设二面角![]() 的大小为
的大小为![]() ,直线
,直线![]() ,
,![]() 与平面
与平面![]() 中所成的角分别为
中所成的角分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地棚户区改造建筑平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形![]() 是原棚户区建筑用地,测量可知边界
是原棚户区建筑用地,测量可知边界![]() 万米,
万米,![]() 万米,
万米,![]() 万米.
万米.
(1)请计算原棚户区建筑用地![]() 的面积及
的面积及![]() 的长;
的长;
(2)因地理条件的限制,边界![]() 不能更改,而边界
不能更改,而边界![]() 可以调整,为了提高棚户区建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区建筑用地的利用率,请在圆弧![]() 上设计一点
上设计一点![]() ,使得棚户区改造后的新建筑用地
,使得棚户区改造后的新建筑用地![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:![]() .
.
(1)求圆的圆心C的坐标和半径长;
(2)直线l经过坐标原点且不与y轴重合,l与圆C相交于![]() 两点,求证:
两点,求证:![]() 为定值;
为定值;
(3)斜率为1的直线m与圆C相交于D、E两点,求直线m的方程,使![]() 的面积最大.
的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.![]() ,
,![]() ,
,![]() 且点
且点![]() 为
为![]() 的中点.
的中点.
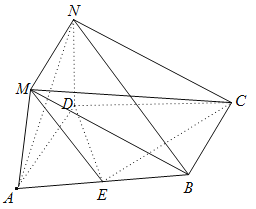
(1) 求证:![]()
![]() 平面
平面![]() ;
;
(2) 求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com