Question

【题目】已知在矩形中，，沿直线BD将△ABD折成，使得点在平面上的射影在内（不含边界），设二面角的大小为，直线 ,与平面中所成的角分别为，则（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

由题意画出图形，由两种特殊位置得到点A′在平面BCD上的射影的情况，由线段的长度关系可得三个角的正弦的大小，则答案可求．

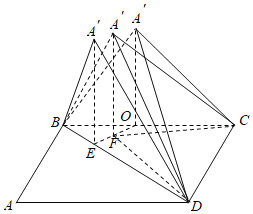
如图，∵四边形ABCD为矩形，∴BA′⊥A′D，

当A′点在底面上的射影O落在BC上时，

有平面A′BC⊥底面BCD，又DC⊥BC，可得DC⊥平面A′BC，则DC⊥BA′，

∴BA′⊥平面A′DC，在Rt△BA′C中，设BA′=1，则BC=，∴A′C=1，说明O为BC的中点；

当A′点在底面上的射影E落在BD上时，可知A′E⊥BD，

设BA′=1，则，∴A′E=，BE=．

要使点A′在平面BCD上的射影F在△BCD内（不含边界），则点A′的射影F落在线段OE上（不含端点）．

可知∠A′EF为二面角A′﹣BD﹣C的平面角θ，

直线A′D与平面BCD所成的角为∠A′DF=α，

直线A′C与平面BCD所成的角为∠A′CF=β，

可求得DF＞CF，∴A′C＜A′D，且，而A′C的最小值为1，

∴sin∠A′DF＜sin∠A′CF＜sin∠A′EO，则α＜β＜θ．

故选D．