
分析 在三角形PF1F2中,由平分线定理,结合椭圆的定义可得$\frac{c}{a}$=$\frac{{F}_{1}M}{P{F}_{1}}$,又在△PF1M和△PF2M中,由余弦定理和诱导公式以及椭圆的定义,化简整理可得得$\frac{{F}_{1}M}{P{F}_{1}}$=$\frac{a}{2c}$,由离心率公式计算即可得到所求值.
解答 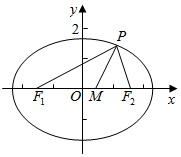 解:在三角形PF1F2中,由平分线定理,可得
解:在三角形PF1F2中,由平分线定理,可得
$\frac{P{F}_{1}}{P{F}_{2}}$=$\frac{{F}_{1}M}{{F}_{2}M}$,即有$\frac{P{F}_{1}}{P{F}_{1}+P{F}_{2}}$=$\frac{{F}_{1}M}{{F}_{1}M+{F}_{2}M}$,
由椭圆的定义可得,
$\frac{P{F}_{1}}{2a}$=$\frac{{F}_{1}M}{2c}$,即$\frac{c}{a}$=$\frac{{F}_{1}M}{P{F}_{1}}$,
又在△PF1M和△PF2M中,
由余弦定理可得,
cos∠F1MP=$\frac{P{M}^{2}+{F}_{1}{M}^{2}-P{{F}_{1}}^{2}}{2PM•{F}_{1}M}$,
cos∠F2MP=$\frac{P{M}^{2}+{F}_{2}{M}^{2}-P{{F}_{2}}^{2}}{2PM•{F}_{2}M}$,
由cos∠F1MP+cos∠F2MP=0,
化简可得PM2•(PF1+PF2)=PF1•F2M2+PF2•F1M2,
结合PF1+PF2=2a,PF1•F2M=PF2•F1M,2PM2=PF1•PF2,
即有2a•PM2=PF2•F1M•2c,
即$\frac{{F}_{1}M}{P{F}_{1}}$=$\frac{a}{2c}$,
可得$\frac{c}{a}$=$\frac{a}{2c}$,即c=$\frac{\sqrt{2}}{2}$a,
可得e=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的离心率的求法,注意运用内角平分线定理和三角形的余弦定理,考查化简整理的运算能力,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | $\frac{11}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{29}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C丄侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°,AB⊥AA1,H为棱CC1的中点,D在棱BB1上,且A1D丄平面AB1H.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C丄侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°,AB⊥AA1,H为棱CC1的中点,D在棱BB1上,且A1D丄平面AB1H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
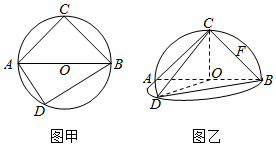 如图甲:⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=$\frac{π}{4}$,∠DAB=$\frac{π}{3}$,沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,根据图乙解答下列各题:
如图甲:⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=$\frac{π}{4}$,∠DAB=$\frac{π}{3}$,沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,根据图乙解答下列各题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知正方体ABCD-A1B1C1D1,点E为棱AA1的中点,则异面直线B1D1与DE所成角的大小是arccos$\frac{\sqrt{10}}{5}$(结果用反三角函数值表示)
已知正方体ABCD-A1B1C1D1,点E为棱AA1的中点,则异面直线B1D1与DE所成角的大小是arccos$\frac{\sqrt{10}}{5}$(结果用反三角函数值表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com