
用0,1,3,5,7五个数字,可以组成多少个没有重复数字且5不在十位位置上的五位数?
解 (1)符合要求的四位偶数可分为三类:
第一类:0在个位时有A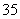 个;
个;
第二类:2在个位时,首位从1,3,4,5中选定1个(A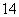 种),十位和百位从余下的数字中选(有A
种),十位和百位从余下的数字中选(有A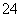 种),于是有A
种),于是有A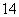 ·A
·A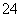 个;
个;
第三类:4在个位时,与第二类同理,也有A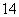 ·A
·A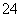 个.
个.
由分类计数原理知,共有四位偶数为A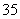 +A
+A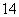 ·A
·A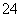 +A
+A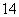 ·A
·A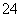 =156(个).
=156(个).
( 2)五位
2)五位 数中5的倍数的数可分为两类:个位数字是0的五位数是A
数中5的倍数的数可分为两类:个位数字是0的五位数是A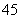 个;个位数字是5的五位数有A
个;个位数字是5的五位数有A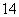 ·A
·A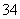 个.
个.
故满足条件的五位数共有A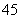 +A
+A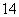 ·A
·A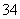 =216(个).
=216(个).
(3)比1 325大的四位数可分为三类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共有A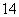 ·A
·A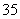 个
个 ;
;
第二类:形如14□□,15□□,共有A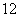 ·A
·A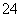 个;
个;
第三类:形如134□,13 5□,共有A
5□,共有A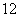 ·A
·A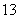 个.
个.
由分类计数原理知,比1 325大 的四位数共有
的四位数共有
 =270(个).
=270(个).


科目:高中数学 来源:2014-2015学年山东省日照市高三3月模拟考试理科数学试卷(解析版) 题型:选择题
运行如图所示的程序框图,则输出的结果S为( )
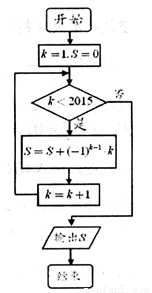
A.1008 B.2015 C.1007 D.
查看答案和解析>>
科目:高中数学 来源: 题型:
电视台在“ 欢乐今宵”节目中拿出两个信箱,其中存放着先后两
欢乐今宵”节目中拿出两个信箱,其中存放着先后两 次竞猜中成绩优秀的观众来信
次竞猜中成绩优秀的观众来信 ,甲信箱中有30封,乙信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的选择?
,甲信箱中有30封,乙信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的选择?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com