
分析 (1)将m=1,写出h(x)的解析式,由基本不等式可知h(x)≥2,h(x)的值域[2,$\frac{26}{5}$];
(2)求导,讨论m取值范围,判断函数的递增区间,
(3)通过解不等式,比较出h(x)与h(4x)的大小,求出m(x)的解析式;求出M1(x),M2(x)求出M1(x)-M2(x)的值域,求出t,n的范围.
解答 解:(1)m=1时,h(x)=x+$\frac{1}{x}$,x∈[$\frac{1}{4}$,5],
h(x)的值域[2,$\frac{26}{5}$];
(2)∵$h′(x)=1-\frac{m}{{x}^{2}}$
①m<0时,h(x)在[$\frac{1}{4},5$]递增;
②$0<m≤\frac{1}{16}$时,h(x)在[$\frac{1}{4},5$]递增;
③$\frac{1}{16}<m≤25$时,h(x)在[$\sqrt{m},5$]递增;
(3)(理)由题知:$h(x)-h(4x)=\frac{3(1-4{x}^{2})}{4x}$,
∴h(x)>h(4x),$x∈[\frac{1}{4},\frac{1}{2})$;
h(x)=h(4x),$x∈\{\frac{1}{2}\}$;
h(x)<h(4x),$x∈(\frac{1}{2},\frac{5}{4}]$.
∵$M(x)=\left\{\begin{array}{l}{h(x)}&{h(x)≥h(4x)}\\{h(4x)}&{h(x)<h(4x)}\end{array}\right.$,
∴$M(x)=\left\{\begin{array}{l}{x+\frac{1}{x}}&{x∈[\frac{1}{4},\frac{1}{2}]}\\{4x+\frac{1}{4x}}&{x∈[\frac{1}{2},\frac{5}{4}]}\end{array}\right.$;
${M}_{1}(x)=\left\{\begin{array}{l}{x+\frac{1}{x},}&{x∈[\frac{1}{4},\frac{1}{2}]}\\{\frac{5}{2},}&{x∈[\frac{1}{2},\frac{5}{4}]}\end{array}\right.$;
${M}_{2}(x)=\left\{\begin{array}{l}{\frac{17}{4},}&{x∈[\frac{1}{4},1]}\\{4x+\frac{1}{4x},}&{x∈[1,\frac{5}{4}]}\end{array}\right.$
${M}_{1}-{M}_{2}\left\{\begin{array}{l}{x+\frac{1}{x}-\frac{17}{4},}&{x∈[\frac{1}{4},\frac{1}{2}]}\\{-\frac{7}{4},}&{x∈[\frac{1}{2},1]}\\{\frac{5}{2}-(4x+\frac{1}{4x}),}&{x∈[1,\frac{5}{4}]}\end{array}\right.$;
${M}_{1}(x)-{M}_{2}(x)∈[-\frac{21}{10},0]$
∴n≥0,$t≤-\frac{21}{10}$;
(3)(文)${h}_{1}(x)=\left\{\begin{array}{l}{x+\frac{1}{x},}&{x∈[\frac{1}{4},1]}\\{2,}&{x∈[1,5]}\end{array}\right.$,${h}_{2}(x)=\left\{\begin{array}{l}{\frac{17}{4},}&{x∈[\frac{1}{4},4]}\\{x+\frac{1}{x},}&{x∈[4,5]}\end{array}\right.$;
${h}_{1}(x)-{h}_{2}(x)=\left\{\begin{array}{l}{x+\frac{1}{x}-\frac{17}{4},}&{x∈[\frac{1}{4},1]}\\{-\frac{9}{4},}&{x∈[1,4]}\\{2-x-\frac{1}{x},}&{x∈[4,5]}\end{array}\right.$,
∴$丨{h}_{1}(x)-{h}_{2}(x)丨∈[0,\frac{16}{5}]$,
∴$n≥\frac{16}{5}$.
点评 本题考查抽象函数的定义域的求法:知f(x)的定义域为[a,b],求f(mx+n)的定义域只要解不等式a≤mx+n≤b即可、考查研究函数的单调区间时,若含参数一般需要讨论.分段函数的处理方法是先分再合的策略,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
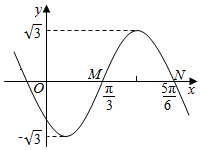 如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.
如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com