
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,M为
,M为![]() 上的一点,以
上的一点,以![]() 为折痕把
为折痕把![]() 折起,使点D到达点P的位置,且平面
折起,使点D到达点P的位置,且平面![]() 平面
平面![]() .连接
.连接![]() ,
,![]() ,点N为
,点N为![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
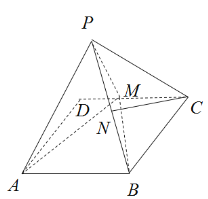
(1)求线段![]() 的长;
的长;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 、
、![]() 满足
满足![]() ,
,![]() .
.
(1)若数列![]() 是等比数列,试判断数列
是等比数列,试判断数列![]() 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(2)若![]() 恰好是一个等差数列的前
恰好是一个等差数列的前![]() 项和,求证:数列
项和,求证:数列![]() 是等差数列;
是等差数列;
(3)若数列![]() 是各项均为正数的等比数列,数列
是各项均为正数的等比数列,数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,经过左焦点
,经过左焦点![]() 的最短弦长为3,离心率为
的最短弦长为3,离心率为![]()
(1)求椭圆的标准方程;
(2)过![]() 的直线与
的直线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与椭圆交于点
,与椭圆交于点![]() ,
,![]() 轴,过
轴,过![]() 的另一直线与椭圆交于
的另一直线与椭圆交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
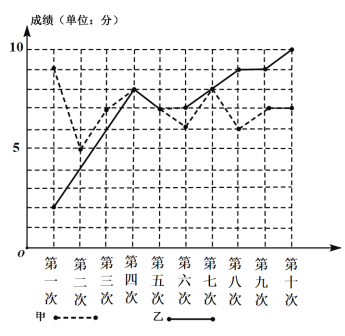
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于曲线![]() ,有下述四个结论:
,有下述四个结论:
①曲线C是轴对称图形;
②曲线C关于点![]() 中心对称;
中心对称;
③曲线C上的点到坐标原点的距离最小值是![]() ;
;
④曲线C与坐标轴围成的图形的面积不大于![]() ,
,
其中所有正确结论的编号是( )
A.①③B.①④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
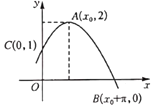
【题目】已知函数![]() 的部分图象如图所示,若将函数
的部分图象如图所示,若将函数![]() 的图象纵坐标不变,横坐标缩短到原来的
的图象纵坐标不变,横坐标缩短到原来的![]() ,再向右平移
,再向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列命题正确的是( ).
的图象,则下列命题正确的是( ).
A.函数![]() 的解析式为
的解析式为![]()
B.函数![]() 的解析式为
的解析式为![]()
C.函数![]() 图象的一条对称轴是直线
图象的一条对称轴是直线![]()
D.函数![]() 在区间
在区间![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]()
![]() 的四个顶点围成的四边形面积为
的四个顶点围成的四边形面积为![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的短轴端点.
的短轴端点.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 过椭圆
过椭圆![]() 的右焦点作互相垂直的两条直线分别与椭圆
的右焦点作互相垂直的两条直线分别与椭圆![]() 相交于
相交于![]() ,
,![]() 和
和![]() ,
,![]() 四点,求四边形
四点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com