
分析 (Ⅰ)通过Sn=n2+n,令n=1可得a1=2,令n≥2可得an=Sn-Sn-1=2n,进而可得an=2n;代入${log_2}{b_n}+\frac{1}{2}{a_n}=0$得${b_n}={(\frac{1}{2})^n}$;
(Ⅱ)通过an=2n、${b_n}={(\frac{1}{2})^n}$可得${c_n}={a_n}{b_n}=n{(\frac{1}{2})^{n-1}}$,利用错位相减法及等比数列的求和公式计算即得结论.
解答 解:(Ⅰ)当n=1时,S1=2,即a1=2,
当n≥2时,an=Sn-Sn-1=2n,
又a1=2=2×1,∴an=2n;
由${log_2}{b_n}+\frac{1}{2}{a_n}=0$得:${b_n}={(\frac{1}{2})^n}$;
(Ⅱ)∵an=2n,${b_n}={(\frac{1}{2})^n}$,
∴${c_n}={a_n}{b_n}=n{(\frac{1}{2})^{n-1}}$,
∴${T_n}=1×{(\frac{1}{2})^0}+2×{(\frac{1}{2})^1}+3×{(\frac{1}{2})^2}+$…$+(n-1)×{(\frac{1}{2})^{n-2}}+n×{(\frac{1}{2})^{n-1}}$,…(1)
$\frac{1}{2}{T_n}=1×{(\frac{1}{2})^1}+2×{(\frac{1}{2})^2}+$…$+(n-1)×{(\frac{1}{2})^{n-1}}+n×{(\frac{1}{2})^n}$,…(2)
(1)-(2)得:$\frac{1}{2}{T_n}=1+{(\frac{1}{2})^1}+{(\frac{1}{2})^2}+$…$+{(\frac{1}{2})^{n-1}}-n×{(\frac{1}{2})^n}=\frac{{1-{{(\frac{1}{2})}^n}}}{{1-\frac{1}{2}}}-n×{(\frac{1}{2})^n}$,
∴${T_n}=4-{(\frac{1}{2})^{n-1}}(n+2)$.
点评 本题考查求数列的通项及求和,考查运算求解能力,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
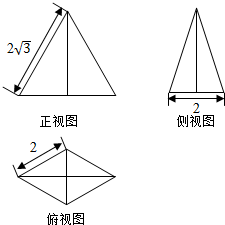 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | (2,2) | C. | (2,1) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | B⊆A | B. | A⊆B | C. | A=B | D. | A∩B=Φ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com