练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知a＞0，b＞0，$a+b=\frac{1}{a}+\frac{1}{b}$，则$\frac{1}{a}+\frac{2}{b}$的最小值为（　　）
    A．4B．$2\sqrt{2}$C．8D．16

    分析 先求出ab=1，从而求出$\frac{1}{a}+\frac{2}{b}$的最小值即可．

    解答 解：由$a+b=\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}$，有ab=1，
    则$\frac{1}{a}+\frac{2}{b}$$≥2\sqrt{\frac{1}{a}×\frac{2}{b}}=2\sqrt{2}$，
    故选：B．

    点评 本题考查了基本不等式的性质，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

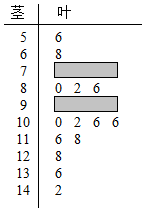    10．某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：
    分数段（分）[50，70）[70，90）[90，110）[110，130）[130，150）总计
    频数b
    频率a0.25
    （Ⅰ）求表中a，b的值及成绩在[90，110）范围内的个体数；
    （Ⅱ）从样本中成绩在[100，130）内的个体中随机抽取4个个体，设其中成绩在[100，110）内的个体数为X，求X的分布列及数学期望E（X）；
    （Ⅲ）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取3个，求其中恰好有1个成绩及格的概率（成绩在[90，150）内为及格）．
    附注：假定逐次抽取，且各次抽取互相独立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

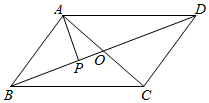
    11．如图，在平行四边形ABCD中，AP⊥BD于点P，且$\overrightarrow{AP}$•$\overrightarrow{AC}$=18，则AP=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设函数f（x）=log7$\frac{x+3}{x-1}$，g（x）=log7（x-1）+log7（5-x），F（x）=f（x）+g（x）
    （1）求函数F（x）的定义域；
    （2）若F（a）＞1，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设x是虚数单位，如果复数$\frac{a+i}{2-i}$的实部与虚部相等，那么实数a的值为（　　）
    A．$\frac{1}{3}$B．$-\frac{1}{3}$C．3D．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=4cosxsin（x-$\frac{π}{6}}$），x∈R．
    （Ⅰ）求f（x）的最小正周期；
    （Ⅱ）在△ABC中，BC=4，sinC=2sinB，若f（x）的最大值为f（ A），求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知f（x）=|x-2|+|x+1|+2|x+2|．
    （1）求证：f（x）≥5；
    （2）若对任意实数x，15-2f（x）＜a2+$\frac{9}{{{a^2}+1}}$都成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数$f（x）=Asin（wx+φ）（A＞0，w＞0，|φ|）＜\frac{π}{2}）$的图象的一个最高点的坐标为$（\frac{π}{6}，2）$，与其相邻的一个最低点的坐标为$（\frac{2π}{3}，-2）$
    （1）求函数f（x）的解析式；
    （2）求函数f（x）的单调增区间及对称轴方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

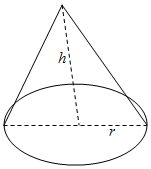    10．如图，某边路清扫机构为预备融化道路积雪，需要在冬天储备$\frac{500}{3}$π（m3）的工业食盐，其食盐堆成底面半径为r（m），高为h（m）的圆锥，并用防水材料S（m2）遮蔽食盐（不考虑接缝与重叠，即面积与圆锥侧面积相同）
    （1）用h来表示S；
    （2）为使得所用遮蔽的防水材料最少，其圆锥形的底面半径应为多少？此时所用防水材料的表面积为多少？

    查看答案和解析>>

    同步练习册答案