Question

8．已知函数f（x）=$\left\{\begin{array}{l}{x+\frac{4}{x}（x＞0）}\\{{x}^{3}+4（x≤0）}\end{array}\right.$，若关于x的方程f（x²）=a（a∈R）有四个不同的实根，则a的取值范围是（　　）

• A． （4，+∞）
• B． [4，+∞）
• C． （-∞，4）
• D． （4，7）

Answer 1

分析 令t=x²，则t≥0，函数f（t）=$\left\{\begin{array}{l}{t+\frac{4}{t}，t＞0}\\{{t}^{3}+4，t≤0}\end{array}\right.$，由题意可得，函数f（t）的图象与直线y=a有4个不同的交点，且每个t值有2个x值与之对应，数形结合可得a的取值范围．

解答 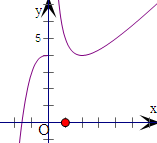解：令t=x²，则t≥0，
函数f（t）=$\left\{\begin{array}{l}{t+\frac{4}{t}，t＞0}\\{{t}^{3}+4，t≤0}\end{array}\right.$．
由题意可得，函数f（t）的图象与直线y=a有2个不同的交点，
且每个t值有2个x值与之对应，如图所示：
由于当t=2时，f（t）=4，
当a＞4时，有两个t值，即有4个不同的实根．
故选A．

点评 本题主要考查函数的零点与方程的根的关系，体现了数形结合的数学思想及等价转化的数学思想，属于中档题．