
分析 把已知数列递推式两边取常用对数,然后构造等比数列,求出数列{an}的通项公式,则极限可求.
解答 解:由an+1=9•$\root{3}{{a}_{n}}$(n≥1),得$lg{a}_{n+1}=lg9+lg\root{3}{{a}_{n}}$,
即$lg{a}_{n+1}=\frac{1}{3}lg{a}_{n}+2lg3$,令bn=lgan,
则${b}_{n+1}=\frac{1}{3}{b}_{n}+2lg3$,∴${b}_{n+1}-3lg3=\frac{1}{3}({b}_{n}-3lg3)$,
则数列{bn-3lg3}是以b1-3lg3=lga1-3lg3=-2lg3为首项,以$\frac{1}{3}$为公比的等比数列,
∴${b}_{n}-3lg3=-2lg3•(\frac{1}{3})^{n-1}$,即${b}_{n}=3lg3-2lg3•(\frac{1}{3})^{n-1}$,
∴${a}_{n}=1{0}^{3lg3-2lg3•(\frac{1}{3})^{n-1}}$,
则$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}1{0}^{3lg3-2lg3•(\frac{1}{3})^{n-1}}$=103lg3=10lg27=27.
故答案为:27.
点评 本题考查数列极限的求法,考查了构造等比数列的方法,训练了等比数列通项公式的求法,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | φ | B. | 45°+φ | C. | 135°-φ | D. | φ-45° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2f(2)>3f(3) | B. | 2f(2)<3f(3) | C. | 2f(2)=3f(3) | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
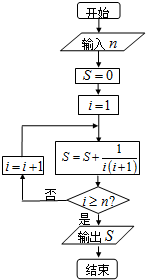
| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{98}{99}$ | D. | $\frac{97}{98}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,点D是AB的中点.
如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
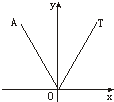
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 以上全不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com