Question

19．如图，在直角坐标系内，射线OT落在60°的终边上，任作一条射线OA，则射线落在∠xOT内的概率是（　　）

• A． $\frac{1}{6}$
• B． $\frac{1}{5}$
• C． $\frac{1}{4}$
• D． 以上全不对

Answer 1

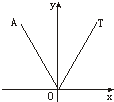
分析 根据周角等于360°，得到所有的基本事件对应的图形是360°角的整个平面区域，再根据射线OT落在60°的终边上，得到符合题意的事件对应的图形是所成角为60°的两条射线之间区域．最后用符合题意的图形对应的角度，除以所有的基本事件对应图形的角度，可得OA落在∠xOT内的概率．

解答 解：∵周角等于360°，
∴任作一条射线OA，它的运动轨迹可以绕原点旋转一周，
所以所有的基本事件对应的图形是360°角的整个平面区域．
∵射线OT落在60°的终边上，
∴若OA落在∠xOT内，符合题意的事件对应的图形是所成角为60°的两条射线之间区域，
记事件X=“任作一条射线OA，OA落在∠xOT内”，
可得所求的概率为：P（x）=$\frac{60}{360}$=$\frac{1}{6}$．
故选：A．

点评 本题以作一条射线，求落在指定区域的事件概率为载体，着重考查了用几何图形求概率的知识，属于基础题．